Поскольку сообщение источника генерируется случайным образом, далее предполагается, что алгебра сообщений аналогична алгебре случайных событий.
Пусть источник может передавать n несовместных 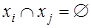 и независимых
и независимых 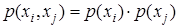 сообщений
сообщений 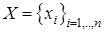 с вероятностями
с вероятностями 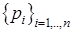 . Количество информации, содержащееся в сообщении
. Количество информации, содержащееся в сообщении 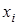 составляет
составляет
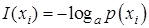
Единицы измерения информации зависят от величины a и носят соответственно названия 2 – бит, е – нит, 10 – дит. Однако, поскольку логарифмы переменной по разным основаниям различаются константой независимо от значения переменной
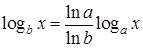
в теории информации принято обозначение log x, которое означает логарифмическую зависимость по произвольному основанию, где масштаб и единицы численного результата определяются основанием логарифмирования.
Количество информации, содержащееся в сообщении 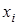 также носит название полной энтропии сообщения
также носит название полной энтропии сообщения 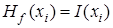 .
.
Изначально понятие энтропии было введено в термодинамике как мера неупорядоченности или хаоса системы и определяется как
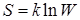
где k – постоянная Больцмана, W – статистический вес системы или количество микросостояний системы, которыми может реализовываться заданное макросостояние.
1
| 1
| 2
| |||||
2
| 2
| 1
|
а) б)
Рис. 1
На рис.1 приведены макросостояния системы со статистическим весом: W =1 – а) обе молекулы слева от перегородки и W = 2 – б) молекулы по разные стороны от перегородки. Второй закон термодинамики запрещает самопроизвольное протекание процессов, сопровождающихся уменьшением энтропии, например передачу тепла от горячего тела к холодному, или диффузию молекул из области высокой концентрации в область низкой.
Среднее количество информации, которое несется сообщением источника (мера его непредсказуемости) носит название средней удельной энтропии, которую мы в дальнейшем будем просто называть энтропией источника
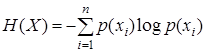 .
.
Слагаемые данного выражения 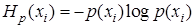 носят название частных энтропий.
носят название частных энтропий.
Свойства энтропии:
- 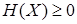 , при чем
, при чем 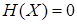 , если источник генерирует единственное детерминированное сообщение;
, если источник генерирует единственное детерминированное сообщение;
- при заданном n энтропия источника максимальна, если сообщения равновероятны и статистически независимы и составляет
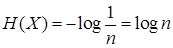 .
.
Покажем, что для источника из двух сообщений, его энтропия максимальна, если сообщения равновероятны.
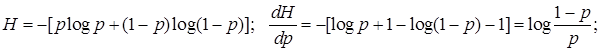
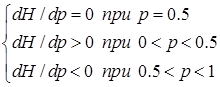
 2014-02-12
2014-02-12 484
484








