Энтропия опытов с неравновероятными взаимонезависимыми сходами

Предположим, что опыт – это генерация источником случайных последовательностей элементов (сигналов) с признаками 1, 2, 3…m. Число различимых элементов называют объемом алфавита источника. Заметим, что статистические свойства источника неизменные, поэтому вероятности появления элементов 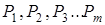в последовательностях достаточно большой длины n также можно считать неизменными.

Согласно теореме об умножении вероятностей для опыта со случайными неравновероятными и взаимонезависимыми исходами средняя вероятность появления любой последовательности сигналов источника длиной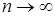

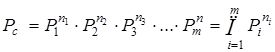(1.8)

Где 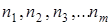– числа элементов с признаками 1, 2, 3…m в последовательности длиной n.

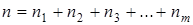
и при этом

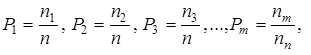
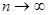(1.9)

Заметим, что число возможных последовательностей N здесь определяется как все размещения с повторениями из n по m

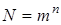
Так как для данного источника 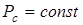, к нему возможно применить для вычисления среднего значения энтропии выражение в форме 1.2

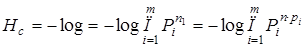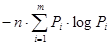=бит/последоват. (1.10)

Величина

Н_сэ=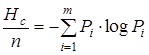бит/элемент (1.11)

Называется средней удельной энтропией многоэлементного источника.

В расчетах информационных характеристик систем широко используется понятие частной энтропии

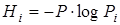бит/исход (1.12)

При реализации конкретного исхода опыта получают количество информации

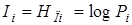бит/исход (1.13)

И 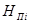называют полной энтропией на "I" исход опыта.