2014-02-12
339
На основе вышеизложенной трактовки событий как множеств сформулируем аксиомы теории вероятностей. Пусть каждому событию А ставится в соответствие некоторое число, называемое вероятностью события. Вероятность события А будем обозначать Р(А). Так как любое событие есть множество, то вероятность события есть функция множества.
Аксиомы ТВ
Свойства операций сложения и умножения
Операций сложения и умножения событий обладают следующими свойствами:
· коммутативностью:
A+B = B+A;
A ∙ B = B ∙ A;
· ассоциативностью :
(A+B)+ C = A +(B+C);
(A ∙ B) ∙ C = A ∙ (B ∙ C);
· дистрибутивностью:
А ∙ (A+B) = A ∙ В +B ∙ C.
Полезные формулы:
· для Ø-события: A + Ø = A; A ∙ Ø = Ø;
· для U -события: A + U = U; A ∙ U = A;
· для А -события: A + A = A; A ∙ A = A.
аксиомам:
1. Вероятность любого события заключена между нулем и единицей:
0 £ Р(А) £ 1
2. Если А и В несовместные события (АВ=Æ), то
Р(А+В) = Р(А) + Р(В)
Эта аксиома легко обобщается (с помощью сочетательного свойства сложения) на любое число событий: если АiАj = Æ при i ¹ j, то
|
|
|
= 
,
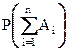
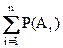т. е. вероятность суммы несовместных событий равна сумме их вероятностей.
Аксиому сложения вероятностей иногда называют «теоремой сложения» (для опытов, сводящихся к схеме случаев, она может быть доказана), а также правилом сложения вероятностей.
3. Если имеется счетное множество несовместных событий A1, A2,..., An,
. (AiAj = Æ при i ¹ j), то
= 
.
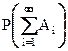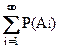Третью аксиому приходится вводить отдельно, так как она не выводится из второй.
Из аксиом 1,2,3 вытекает ряд важных следствий.
Следствие 1. Сумма вероятностей полной группы несовместимых событий равна единице, т.е. если
S Ai = Ω; AiAj = Æ при i ¹ j, то
S 
P(Ai) = 1.
Доказательство: действительно, так как события A1, A2,..., An несовместны, то к ним применимо правило сложения:
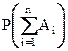= P ∑ (Ai) = P(Ω) = 1.
