Решение
По определению
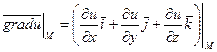
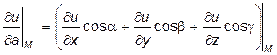
Предварительно найдем значение частных производных в точке 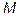 и направляющие косинусы вектора:
и направляющие косинусы вектора: 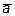 .
.
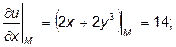
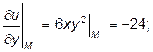
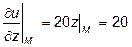
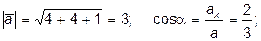
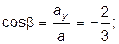
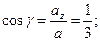
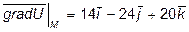 ,
,
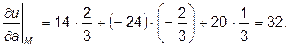
Задача 5.4 Определить размеры прямоугольного параллелепипеда с диагональю 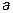 , имеющего максимальный объем.
, имеющего максимальный объем.
Пусть 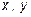 и
и 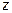 - длины ребер параллелепипеда. Тогда его объем
- длины ребер параллелепипеда. Тогда его объем
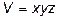 .
.
Так как 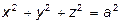 , то
, то 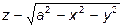 и
и 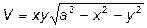 .
.
Очевидно, что 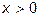 ,
, 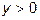 ,
, 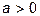 ,
, 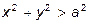 .
.
Множество точек 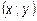 , удовлетворяющих этим требованиям, можно изобразить так (рис.5.1.):
, удовлетворяющих этим требованиям, можно изобразить так (рис.5.1.):
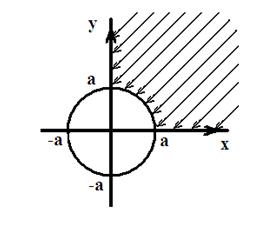
Рис. 5.1.
Для нахождения точек экстремума приравняем к нулю частные похідні функции 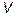 :
:
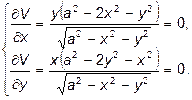
Отсюда
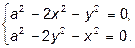
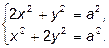
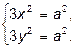
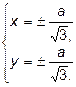
Итак, имеем 4 критические точки:
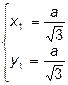 ;
; 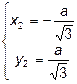 ;
; 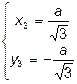 ;
; 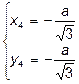
Условию задачи удовлетворяет только первая точка 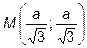 .
.
Проверим выполнение в этой точке достаточного условия существования экстремума.
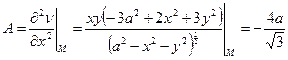 ;
;
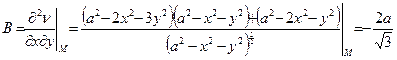 ;
;
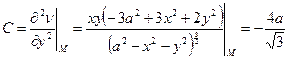 .
.
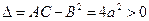
Следовательно, в точке 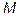 существует экстремум, а именно максимум
существует экстремум, а именно максимум 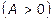 .
.
Зная 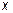 и
и 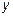 , найдем
, найдем 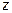 :
:
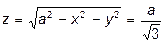
Значит, 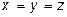 .
.
Итак, изо всех прямоугольных параллелепипедов с фиксированной диагональю максимальный объем имеет куб с ребром, равным 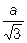 .
.
 2014-02-12
2014-02-12 411
411







