Теоретико-множественные операторы

6.1. Обзор реляционной алгебры

Замкнутость реляционной алгебры

Реляционная алгебра представляет собой набор операторов, использующих отношения в качестве аргументов, и возвращающие отношения в качестве результата. Таким образом, реляционный оператор 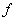выглядит как функция с отношениями в качестве аргументов: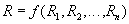

Реляционная алгебра является замкнутой, т.к. в качестве аргументов в реляционные операторы можно подставлять другие реляционные операторы, подходящие по типу:

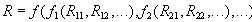
Таким образом, в реляционных выражениях можно использовать вложенные выражения сколь угодно сложной структуры.

Каждое отношение обязано иметь уникальное имя в пределах базы данных. Имя отношения, полученного в результате выполнения реляционной операции, определяется в левой части равенства. Однако можно не требовать наличия имен от отношений, полученных в результате реляционных выражений, если эти отношения подставляются в качестве аргументов в другие реляционные выражения. Такие отношения будем называть неименованными отношениями. Неименованные отношения реально не существуют в базе данных, а только определяются в момент вычисления значения реляционного оператора. Традиционно, вслед за Коддом, определяют восемь реляционных операторов, объединенных в две группы.

Теоретико-множественные операторы:

• Объединение.
• Пересечение.
• Вычитание.
• Декартово произведение.

Специальные реляционные операторы:

• Выборка.
• Проекция.
• Соединение.
• Деление.

Не все они являются независимыми, т.е. некоторые из этих операторов могут быть выражены через другие реляционные операторы.

Отношения, совместимые по типу

Некоторые реляционные операторы (например, объединение) требуют, чтобы отношения имели одинаковые заголовки. Действительно, отношения состоят из заголовка и тела. Операция объединения двух отношений есть просто объединение двух множеств кортежей, взятых из тел соответствующих отношений. Но будет ли результат отношением? Во-первых, если исходные отношения имеют разное количество атрибутов, то, очевидно, что множество, являющееся объединением таких разнотипных кортежей нельзя представить в виде отношения. Во-вторых, пусть даже отношения имеют одинаковое количество атрибутов, но атрибуты имеют различные наименования. Как тогда определить заголовок отношения, полученного в результате объединения множеств кортежей? В-третьих, пусть отношения имеют одинаковое количество атрибутов, атрибуты имеют одинаковые наименования, но определенны на различных доменах. Тогда снова объединение кортежей не будет образовывать отношение.

Определение 1. Будем называть отношения совместимыми по типу, если они имеют идентичные заголовки, а именно:

• Отношения имеют одно и то же множество имен атрибутов, т.е. для любого атрибута в одном отношении найдется атрибут с таким же наименованием в другом отношении.
• Атрибуты с одинаковыми именами определены на одних и тех же доменах.

Некоторые отношения не являются совместимыми по типу, но становятся таковыми после некоторого переименования атрибутов. Для того чтобы такие отношения можно было использовать в реляционных операторах, вводится вспомогательный оператор переименования атрибутов.

Оператор переименования атрибутов

Оператор переименования атрибутов имеет следующий синтаксис:

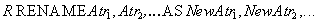
где

- отношение,

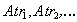- исходные имена атрибутов,

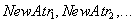- новые имена атрибутов.

В результате применения оператора переименования атрибутов получаем новое отношение, с измененными именами атрибутов.

Пример 1.

Следующий оператор возвращает неименованное отношение, в котором атрибут 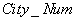переименован в :

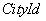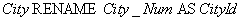
6.2. Теоретико-множественные операторы

6.2.1. Объединение

Определение 2. Объединением двух совместимых по типу отношений и называется отношение с тем же заголовком, что и у отношений и , и телом, состоящим из кортежей, принадлежащих или , или , или обоим отношениям.

Синтаксис операции объединения:

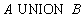
Замечание. Объединение, как и любое отношение, не может содержать одинаковых кортежей. Поэтому, если некоторый кортеж входит и в отношение , и отношение , то в объединение он входит один раз.

Пример 2. Пусть даны два отношения и с информацией о сотрудниках:

Табельный номер	Фамилия	Зарплата
1	Иванов
2	Петров
3	Сидоров

Таблица 1. Отношение A.

Табельный номер	Фамилия	Зарплата
1	Иванов
2	Пушников
4	Сидоров

Таблица 2. Отношение B.

Объединение отношений и будет иметь вид:

Табельный номер	Фамилия	Зарплата
	Иванов
	Петров
	Сидоров
	Пушников
	Сидоров

Таблица 3. Отношение A UNION B.

Замечание. Как видно из приведенного примера, потенциальные ключи, которые были в отношениях и не наследуются объединением этих отношений. Поэтому, в объединении отношений и атрибут "Табельный номер" может содержать дубликаты значений. Если бы это было не так, и ключи наследовались бы, то это противоречило бы понятию объединения как "объединение множеств". Конечно, объединение отношений и имеет, как и любое отношение, потенциальный ключ, например, состоящий из всех атрибутов.

6.2.2. Пересечение

Определение 3. Пересечением двух совместимых по типу отношений и называется отношение с тем же заголовком, что и у отношений и , и телом, состоящим из кортежей, принадлежащих одновременно обоим отношениям и .

Синтаксис операции пересечения:

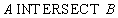
Пример 3. Для тех же отношений и , что и в предыдущем примере пересечение имеет вид:

Табельный номер	Фамилия	Зарплата
	Иванов

Таблица 4. Отношение A INTERSECT B.

Замечание. Казалось бы, что в отличие от операции объединения, потенциальные ключи могли бы наследоваться пересечением отношений. Однако это не так. Вообще, никакие реляционные операторы не передают результирующему отношению никаких данных о потенциальных ключах. В качестве причины этого можно было бы привести тривиальное соображение, что так получается более просто и симметрично - все операторы устроены одинаково. На самом деле причина более глубока, и заключается в том, что потенциальный ключ - семантическое понятие, отражающее различимость объектов предметной области. Наличие потенциальных ключей не выводится из структуры отношения, а явно задается для каждого отношения, исходя из его смысла. Реляционные же операторы являются формальными операциями над отношениями и выполняются одинаково, независимо от смысла данных, содержащихся в отношениях. Поэтому, реляционные операторы ничего не могут "знать" о смысле данных. Трактовка результата реляционных операций - дело пользователя.

6.2.3. Вычитание

Определение 4. Вычитанием двух совместимых по типу отношений и называется отношение с тем же заголовком, что и у отношений и , и телом, состоящим из кортежей, принадлежащих отношению и не принадлежащих отношению .

Синтаксис операции вычитания:

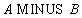
Пример 4. Для тех же отношений и , что и в предыдущем примере вычитание имеет вид:

Табельный номер	Фамилия	Зарплата
2	Петров
3	Сидоров

Таблица 5. Отношение A MINUS B.

6.2.4. Декартово произведение

Определение 5. Декартовым произведением двух отношени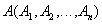й и 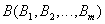называется отношение, заголовок которого является сцеплением заголовков отношений и :

,

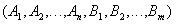а тело состоит из кортежей, являющихся сцеплением кортежей отношений и :

,

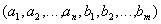таких, что , .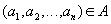

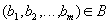Синтаксис операции декартового произведения:

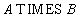
Замечание. Мощность произведения 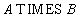равна произведению мощностей отношений и , т.к. каждый кортеж отношения соединяется с каждым кортежем отношения .

Замечание. Если в отношения и имеются атрибуты с одинаковыми наименованиями, то перед выполнением операции декартового произведения такие атрибуты необходимо переименовать.

Замечание. Перемножать можно любые два отношения, совместимость по типу при этом не требуется.

Пример 5. Пусть даны два отношения и с информацией о поставщиках и деталях:

Номер поставщика	Наименование поставщика
1	Иванов
2	Петров
3	Сидоров

Таблица 6. Отношение A (Поставщики).

Номер детали	Наименование детали
1	Болт
2	Гайка
3	Винт

Таблица 7. Отношение B (Детали).

Декартово произведение отношений и будет иметь вид:

Номер поставщика	Наименование поставщика	Номер детали	Наименование детали
	Иванов		Болт
	Иванов		Гайка
	Иванов		Винт
	Петров		Болт
	Петров		Гайка
	Петров		Винт
	Сидоров		Болт
	Сидоров		Гайка
	Сидоров		Винт

Таблица 8. Отношение A TIMES B.

Замечание. Сама по себе операция декартового произведения не очень важна, т.к. она не дает никакой новой информации, по сравнению с исходными отношениями. Для реальных запросов эта операция почти никогда не используется. Однако операция декартового произведения важна для выполнения специальных реляционных операций, о которых речь пойдет ниже.

Лекция 7. Реляционная алгебра. Часть 2.