Можно показать, что
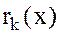 = НОДº(
= НОДº(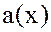 ,
,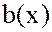 ).
).
Действительно, просмотр равенств (1) снизу вверх показывает, что 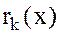 является делителем
является делителем 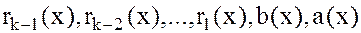 , т.е. общим делителем
, т.е. общим делителем 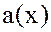 и
и 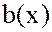 .
.
Просмотр равенств (1) сверху вниз показывает, что все остатки 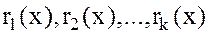 делятся на любой общий делитель
делятся на любой общий делитель 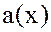 и
и 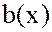 .
.
Докажем вторую часть теоремы.
Предположим, что существуют два НОД
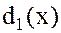 = НОДº(
= НОДº(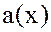 ,
,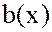 ),
),
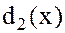 = НОДº(
= НОДº(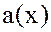 ,
,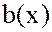 ).
).
Тогда, согласно определению НОДº(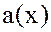 ,
,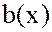 ),
),
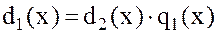
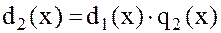
и, с учетом правила
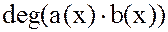 =
=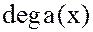 +
+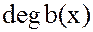 ,
,
имеем
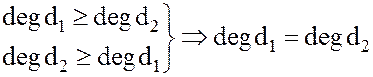
и многочлены 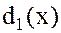 и
и 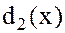 отличаются лишь множителем нулевой степени и, следовательно, наше предположение неверно.
отличаются лишь множителем нулевой степени и, следовательно, наше предположение неверно.
Пример. Пусть заданы два многочлена 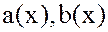
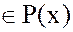 :
:
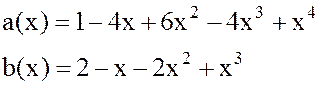
Требуется найти НОДº(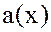 ,
,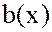 ). Алгоритм поиска НОДº(
). Алгоритм поиска НОДº(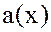 ,
,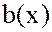 ):
):
 2014-02-13
2014-02-13 232
232







