Динамика производства электроэнергии в регионе

Год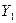
		2,23
		2,46
		2,70
		2,84
		3,02
		3,11
		3,19

Найдя минимальное и максимальное значения логарифмов произ­водства электроэнергии, строим масштаб с таким расчетом, чтобы все данные разместились на графике. В соответствии с масштабом находим соответствующие точки, которые соединим прямыми линиями. В результате получим график (см. рис. 5.18) с использованием логарифмиче­ского масштаба на оси ординат. Поэтому он называется диаграммой на полулогарифмической сетке. Полной логарифмической диаграммой он будет в том случае, если по оси абсцисс будет построен логарифмиче­ский масштаб. В рядах динамики это никогда не применяется, так как логарифмирование времени лишено всякого смысла.

Логарифмы чисел Числа

3,0 1000

0,5 2,5 317

0,5 2,0 100

0,5 1,5 31,7

0,5

1,0 10

Рис. 5.17. Схема логарифмического масштаба

Млрд. кВт/ч

3,2 1585

3 1000

2,8 631

2,6 398

2,4 251

2,2 159

2

год

Рис. 5.18. Динамика производства электроэнергии в регионе за 2002-2007 гг.

К диаграммам динамики относятся и радиальные диаграммы, построенные в полярных координатах и предназначенные для отражения процессов, ритмически повторяющихся во времени (см. рис. 5.19). Чаще всего эти диаграммы применяются для иллюстрации сезонных колебаний, и в этом отношении они имеют преимущество перед статистическими кривыми. Радиальные диаграммы делятся на два вида: замкнутые и спиральные. Эти два вида диаграмм отличаются друг от друга по технике построения, все зависит от того, что взято в качестве базы отсчета – центр круга или окружность.

Замкнутые диаграммы (см. рис. 5.19а) отражают весь внутригодовой цикл динамики какого, либо одного года. Их построение сводит­ся к следующему: вычерчивается круг, среднемесячный показатель при­равнивается к радиусу этого круга, затем весь круг делится на двена­дцать равных секторов, посредством проведения радиусов, которые изо­бражаются в виде тонких линий. Каждый радиус изображает месяц, причем расположение месяцев аналогично циферблату часов. На каж­дом радиусе делается отметка в определенном месте, согласно масшта­бу, исходя из данных на соответствующий месяц. Если данные превы­шают среднегодовой уровень, то отметка делается вне окружности на продолжении радиуса. Затем отметки различных месяцев соединяются отрезками.

Если в качестве базы отсчета берется окружность, такого рода диаграммы называются спиральными (см. рис. 5.196). Спиральные диа­граммы отличаются от замкнутых тем, что в них декабрь одного года соединяется не с январем данного же года, а с январем следующего года. Это дает возможность изобразить весь динамический ряд в виде одной кривой. Особенно наглядна такая диаграмма тогда, когда наряду с сезонным ритмом ряд обнаруживает неуклонный рост из года в год.