А) sinx~x при х→0, т.к. 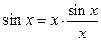 , а
, а 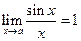 .
.
Б) 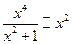 при
при 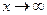 , т.к.
, т.к. 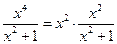 ,
, 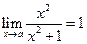 .
.
1)  f – б.м.ф. по сравнению с g при x→a.
f – б.м.ф. по сравнению с g при x→a.
Обозначение: 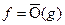 при x→a.
при x→a.
2) 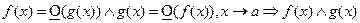 одного порядка (подобны) x→a.
одного порядка (подобны) x→a.
Обозначение: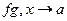
Th. Пусть 
1. 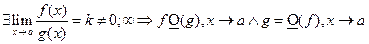 или
или 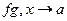 ( подобиязначок);
( подобиязначок);
2. 
3.  (
(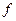 - б.м.ф. более высокого порядка, чем
- б.м.ф. более высокого порядка, чем 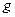 )
)
Док-во:


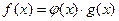 , где
, где 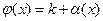 ,
, 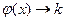 при
при 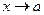
1) 
Аналогично:
0. где 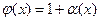 ;
;
1. 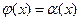 .
.
2. Пусть 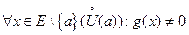 . Тогда
. Тогда  .
.
Док-во:
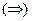 Если
Если 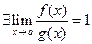 , то
, то
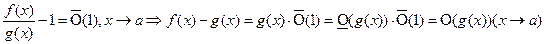 .
.
Поэтому 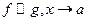 .
.
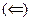 Если
Если 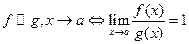 .
.
Если 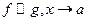 , то согласно определению,
, то согласно определению, 
 .
.
Наиболее содержательные результаты получаются, если 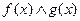 - б.м.ф.
- б.м.ф.
Df 4. Пусть 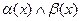 - б.м.ф. при
- б.м.ф. при 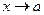 . Тогда если
. Тогда если  (и соответственно
(и соответственно 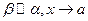 ) – то
) – то 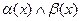 называются эквивалентными б.м. при
называются эквивалентными б.м. при 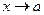 .
.
Th О свойствах символа 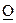
Пусть функции 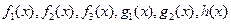 определены на множестве Е и
определены на множестве Е и 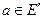 , тогда
, тогда
1) 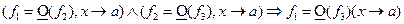 - транзитивность символа
- транзитивность символа 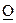 .
.
2) Теорема сложения: 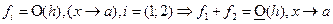 .
.
3) Теорема умножения: 

(б/д)
Следствие. Пусть функции 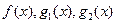 определены на Е и
определены на Е и 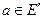 . Тогда
. Тогда
1) 
2) 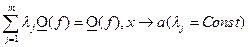 .
.
3) 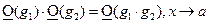
 2014-02-09
2014-02-09 427
427







