Th О свойствах символа O малое

Примеры.

1.

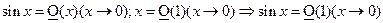
2. .

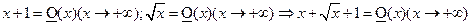Пусть функции 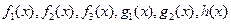определены на Е и . Тогда

I.

a)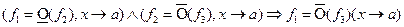

b)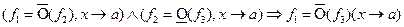

c) Теорема транзитивности.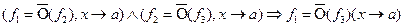

II. Теорема сложения.

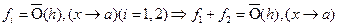
III. Теорема умножения.

.

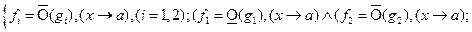
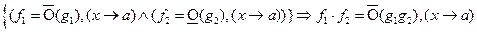Следствие. Пусть функции 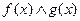определены на Е и 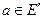. Тогда

1) a);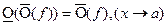

б) ;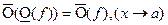

в) ;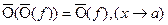

2)

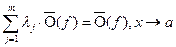
3)

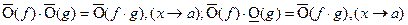
Th (критерии эквивалентности функций)

Для того, чтобы функции 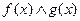были эквивалентными , чтобы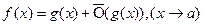

(б/д)

Th Если 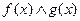определены на Е и 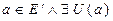, такая, ч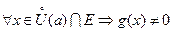то , то 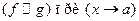означает, что .

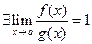Док-во:

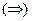Т.к. 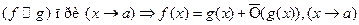, откуда в 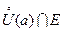имеем

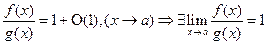
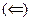Обратное утверждение доказать самостоятельно.