Системы счисления, применяемые в цифровых ЭВМ
В ЭВМ используются следующие системы счисления:
1. Двоичная система счисления - в качестве рабочей;
2. Десятичная система счисления - для записи исходной информации и выдачи результатов;
3. Восьмеричная система счисления;
4. Шестнадцатиричная система счисления;
5. Смешанная (двоично-десятичная) система счисления.
Восьмеричная и шестнадцатиричная системы счисления являются вспомогательными. Они применяются при подготовке задач к решению (программировании на языках ассемблере, машинном и др.). Данные системы удобны тем, что 8-ричная запись какого-либо числа в три раза короче его двоичной записи, а 16-ричная запись - в четыре раза. Что касается перевода чисел из одной системы в другую, а именно по схемам 8®2, 2®8, 16®2, 2®16, то он не вызывает каких-либо затруднений и может выполняться чисто механическим путем.
Двоично-десятичная система счисления также является вспомогательной и используется, в основном, для хранения десятичных чисел в памяти ЭВМ. Запись десятичных чисел в двоично-десятичной с.с. осуществляется следующим образом. Каждая цифра десятичного числа записывается ее двоичным эквивалентом. Для такой записи потребуется не более четырех двоичных разрядов. Четырехзначное двоичное число, изображающее десятичную цифру, называется тетрадой.
Для того чтобы некоторое десятичное число представить в двоично-десятичной форме, необходимо каждую его цифру записать соответствующей ей тетрадой. Возьмем, например, десятичное число 3795,28 и запишем его в двоично-десятичном виде:
3 7 9 5, 2 8
0011 0111 1001 0101, 0010 1000
Т.о., десятичное число 3795,28 будет иметь такую двоично-десятичную запись: 0011011110010101,00101000.
Переход от десятичной к двоично-десятичной записи производится, как видим, элементарно и не требует каких-либо вычислений.
Для обратного перевода (от двоично-десятичной записи к десятичной) необходимо двоично-десятичное число влево и вправо от запятой разбить на четверки цифр (тетрады), а затем каждую из них записать отвечающей ей десятичной цифрой.
Пусть, например, дано двоично-десятичное число: 010110000110,00110111
Разобьем его на тетрады и заменим каждую тетраду десятичной цифрой:
0101 1000 0110, 0011 0111 = 586,37.
Общее правило для перевода целых чисел. Для перевода целого числа из одной позиционной системы счисления в другую, его надо последовательно разделить на основание q той системы, в которую оно переводится. Деление производится до тех пор, пока не получим частное, меньшее чем q. Число в новой системе счисления запишется в виде остатков деления, начиная с последнего. Последнее частное дает старшую цифру числа. Перевод производится в той системе счисления из которой переводим.
Примеры:
1)
|
(3010®N2).
30| 2___
 30 15 | 2___
30 15 | 2___
 0 14 7 | 2___
0 14 7 | 2___

 1 6 3 | 2___
1 6 3 | 2___

 1 2 1 ® Старшая циф-
1 2 1 ® Старшая циф-
 1 ра результата
1 ра результата
30=11102
 |
3) 2810®N16.
28 | 16_
 16 1
16 1
 12
12
Поскольку десятичное число 12 в 16-ричной системе счисления обозначается цифрой (буквой) С, получим: 2810=1С16.
Общее правило для перевода правильных дробей. Для перевода правильной дроби из одной позиционной системы счисления в другую, ее надо последовательно умножить на основание q той системы, в которую оно переводится. Перемножаются только дробные части. Дробь в новой системе запишется в виде целых частей получающихся произведений, начиная с первого.
Примеры.
1)
|
|
|
|
2
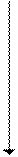
 0,6250
0,6250
2
 1,2500
1,2500
2
 0,5000
0,5000
2
 1,0000
1,0000
0,312510=0,01012.
Этот процесс необязательно будет конечным, как для целых чисел. Он может продолжаться для любого числа значащих цифр. Если получаемая дробь бесконечная, она может быть периодической (иметь повторяющиеся группы цифр - период) или непериодической. Например, десятичная дробь 0,15 выражается периодической дробью вида:
0,15=0,00100110011001...2=0,00(1001) 2.
В скобках указан период двоичной дроби.
Общее правило для перевода неправильных дробей. При переводе неправильных дробей отдельно переводят целую и дробную части по своим правилам.
|
37 | 8__
32 4
5
37=458.
0,41=0,3217...8.
37,4110=45,3217... 8.
Перевод чисел из любой системы счисления в десятичную. Перевод чисел из любой системы счисления в десятичную можно осуществить, используя свойство позиционной системы счисления (представление любого числа в виде многочлена по степеням основания) и выполняя действия над числами, представленными в привычной для нас десятичной системе. Примеры:
1) Дано двоичное число 1011012. Получить его десятичную запись (1011012®N10).
1011012=1·25+0·24+1·23+1·22+0·21+1·20=32+0+8+4+0+1=45.
1011012=4510.
2) 1DA916®N10.
1DA916=1·163+13·162+10·161+9·160=4096+3328+160+9=7593
1DA916=759310.
Если основание p-ичной системы счисления является степенью основания q-ичной системы, т.е. p=qk (k - целое число), то перевод числа из p-ичной системы счисления в q-ичную систему счисления и, наоборот можно выполнить по более простым правилам: переводу каждой цифры в отдельности.
Перевод числа из восьмеричной системы счисления в двоичную и обратно. Т.к. 8=23, то для перевода в 8-ричного числа в двоичную систему счисления достаточно каждую восьмеричную цифру заменить ее двоичным представлением (двоичной триадой).
|
1 - 0012 5 - 1012
2 - 0102 6 - 1102
3 - 0112 7 - 1112
Для обратного перевода (из 2-ичной системы счисления в 8-ричную систему счисления) следует двоичное число разбить на триады влево и вправо от запятой, и каждую триаду заменить соответствующей ей 8-ричной цифрой. Если при разбиении самая левая или самая правая тройки оказываются неполными - их дополняют путем приписывания нулей. Примеры:
1) 1011102=101 1002=568.
2) 11101110,00011112=011 101 110, 000 111 1002=356,0748
Перевод чисел из шестнадцатиричной системы счисления в двоичную и обратно. Т.к. 16=24, то для перевода 16-ричного числа в 2-ичную с.с. достаточно каждую 16-ричную цифру заменить соответствующей ей двоичной тетрадой. Приведем эти тетрады:
|
1 - 0001 9 - 1001
2 - 0010 A - 1010
3 - 0011 B - 1011
4 - 0100 C - 1100
5 - 0101 D - 1101
6 - 0110 E - 1110
7 - 0111 F - 1111
Для обратного перевода (из 2-ичной системы счисления. в 16-ричную систему счисления) следует двоичное число разбить на тетрады влево и вправо от запятой, и каждую тетраду заменить соответствующей ей 16-ричной цифрой. Если при разбиении самая левая или самая правая четверки оказываются неполными - их дополняют путем приписывания нулей. Примеры:
1) 1011102 = 0010 11102 = 2E16. 2) 10111,1012 = 00010111,10102 = 17,A16.
 2014-02-13
2014-02-13 1492
1492
