Рекурсивные функции

Ключевым моментом для определения рекурсивных функций в лямбда-исчислении является существование так называемых комбинаторов неподвижной точки. Замкнутый лямбда-терм Y называется комбинатором неподвижной точки, если для любого лямбда-терма f выполняется: f(Y f) = Y f. Таким образом, комбинатор неподвижной точки по заданному терму f возвращает неподвижную точку f, т.е. терм х, такой что f(x) = х. Первый такой комбинатор, найденный Карри, обычно обозначается как Y. Его называют также «парадоксальным комбинатором». Он определяется следующим образом:

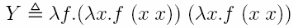
Данное выражение действительно определяет комбинатор неподвижной точки, поскольку:

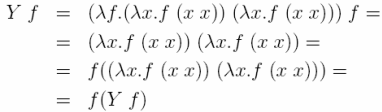
Комбнатор неподвижной точки Кари решает задачу математичеки. Однако, с вычислительной очки зрения такое определение вызывает трудности, поскольку выполняемые проебразования используют лямбда-равенство, а не редукцию, а также обратную β -конверсию. Поэтому для вычислительных целей более предпочтительно определение комбинатора неподвижной точки, принадлежащее Тьюрингу:

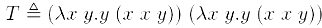
Будем обозначать комбинатор неподвижной точки Тьюринга как Y. Он может быть исползован в определении рекурсивных функций. Рассмотрим в качестве примера функцию факториал:

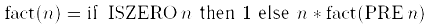
Преобразуем это выражение к следующему эквивалентному виду:

Т.о. fact = F fact, где

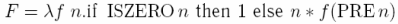
Отсюда можно заключить, что fact является неподвижной точкой функции F т.е., fact = Y F.

Данная техника обобщается для определения взаимно рекурсивных функций, т.е. набора функций, определения которых взаимно зависят друг от друга.

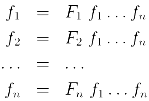
Эти выражения, используя кортежи, можно преобразовать к одному равенству:

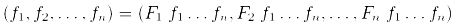
Положив t = (f ₁, f ₂, …, f _n) и введя F = λ q. (F ₁ q, F ₂ q, …, F _n q) получим

t = F t.

Отсюда, снова с помощью селекторов f _i = (t)_i, можно получить отдельные компоненты кортежа t.