Некоторые выражения не имеют типа, например, λf. f f или λf. (f true, f. 1) Типизируемые выражения обычно имеют много типов, хотя некоторые имеют только один.
Имеет место утверждение: для каждого типизируемого выражения существует наиболее общий тип или основной тип, и все возможные типы выражения являются экземплярами этого наиболее общего типа. Прежде чем сделать это утверждение строгим, необходимо ввести некоторую терминологию.
Введем понятие типовых переменных. Типы могут быть сконструированы с помощью применения конструкторов типа либо к типовым константам, либо к переменным. Будем использовать буквы α и β для типовых переменных, а σ и τ - для произвольных типов. Определим понятие замены типовой переменной на некоторый тип. Будем использовать ту же нотацию, что и при подстановке термов. Например:
(σ —> bоо1)[ σ:= (σ —> τ)] = (σ —> τ)—> bool
Расширим это определение, добавив параллельные подстановки:
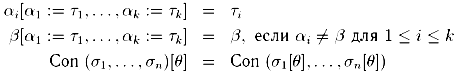
Можно рассматривать типовые константы как 0-арные конструкторы, т. е. считать, что int задается как int (). Имея определение подстановки, можно счиать, что тип σ является более общим, чем тип σ' и записывать этот факт как 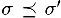 . Это отношение выполняется тогда и только тогда, когда существует набор подстановок θ такой, что σ' = σ θ. Например:
. Это отношение выполняется тогда и только тогда, когда существует набор подстановок θ такой, что σ' = σ θ. Например:
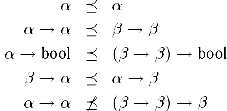
Имеет место:
Теорема 4. Каждый типизируемый терм имеет некоторый основной тип, т. е. если Т:: τ, то существует некоторый σ, такой что Т:: σ и для любого σ', если Т:: σ', то 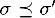 .
.
Доказательство этой теоремы конструктивно: оно дает конкретную процедуру для поиска основного типа. Эта процедура известна как алгоритм Хиндли-Милнера. Все реализации языков программирования типа Haskell включают в себя вариант этого алгоритма. Выражения в них могут быть сопоставлены их основному типу либо отвергнуты как нетипизируемые.
 2014-02-13
2014-02-13 713
713








