Сильная нормализация
Справедлива следующая теорема о сильной нормализации:
Теорема 5. Каждый типизируемый терм имеет нормальную форму и каждая возможная последовательность редукций, начинающаяся с типизируемого терма, завершается.
Функциональная программа, соблюдающая дисциплину типизации, может быть вычислена любым образом, и она всегда завершится в единственной нормальной форме (единственность следует из теоремы Черча-Россера, которая выполняется и для типизированного лямбда-исчисления). Однако возможность создавать незавершающиеся программы существенна для полноты по Тьюрингу для определения произвольных вычислимых и полных функций.
Чтобы обеспечить полноту по Тьюрингу, добавим способ определения произвольных рекурсивных функций, которые являются правильно типизированными. Для этого определим полиморфный оператор рекурсии для всех типов вида:
Rec:: ((σ —> τ) —> (σ —> τ)) —> σ —> τ
Кроме того, добавим правило редукции:
Rec F —> F (Rec F)
для любого F:: (σ —> τ) —> (σ —> τ).
Будем считать, что рекурсивные определения функций интерпретируются с использованием этих операторов рекурсии.
С теоретической точки зрения, нормальный порядок редукции выражений наиболее предпочтителен, поскольку если какая либо стратегия завершается, завершится и она. Такая стратегия известна как вызов по имени. С практической точки зрения такая стратегия имеет существенные недостатки.
Рассмотрим выражение
(λ х. х + х + х) (10 + 5)
Нормальная редукция приводит это выражение к следующему виду:
(10 + 5) + (10 + 5) + (10 + 5)
Таким образом, необходимо трижды вычислять значение одного и того же выражения. На практике это недопустимо. Существуют два основных подхода к решению этой проблемы.
При первом подходе отказываются от нормальной стратегии и вычисляют аргументы функций до того, как передать их значения в функцию. Такой подход называют передачей по значению. При этом вычисление некоторых выражений, завершающееся при нормальной стратегии, может привести к бесконечной последовательности редукций. Однако такая стратегия позволяет получать эффективный машинный код.
При другом подходе, использующемся в Haskell, нормальная стратегия редукций сохраняется. Однако различные возникающие подвыражения разделяются и никогда не вычисляются более одного раза. Такой способ вызова называется ленивым или вызовом по необходимости, поскольку выражения вычисляются только тогда, когда их значения действительно необходимы для работы программы.
Оптимизирующие компиляторы языка Haskell выявляют места программы, в которых можно обойтись без отложенных вычислений.
Конструкторы данных в Haskell можно считать функциями (единственное отличие от функций заключается в том, что их можно использовать в шаблонах при сопоставлении с образцом.) В сочетании с «ленивым» вызовом это позволяет определять бесконечные структуры данных. Примером служит бесконечный список целых чисел, начиная с числа n:
numsFrom n = n: numsFrom (n +1)
Программа, реализующая отложенные вычисления, может быть представлена в виде конструкции g (f input), где g и f - некоторые функции. Они выполняются строго синхронно, f запускается только тогда, когда g требуется прочитать данные. После этого f приостанавливается, и невыполняется, до тех пор пока g вновь не попытается прочитать следующую группу входных данных. Если g заканчивается, не прочитав весь вывод f, то f прерывается, f может быть не завершаемой программой, создающей бесконечный вывод, так как она будет остановлена, как только завершится д. Это позволяет отделить условия завершения от тела цикла, что является мощным средство модуляризации.
Этот метод называется "ленивыми вычислениями" так как f выполняется настолько редко, насколько это возможно. Он позволяет осуществить модуляризацию программы как генератора, который создает большое количество возможных ответов, и селектора, который выбирает подходящие.
Рассмотрим алгоритм Ньютона-Рафсона для вычисления квадратного корня. Этот алгоритм вычисляет квадратный корень числа z, начиная с начального приближения a 0. Он уточняет это значение на каждом последующем шаге, используя правило:
an+1 = (ап + z/an)/2
Если приближения сходятся к некоторому пределу a, то a = (a + z/a)/2, то есть а • а = z или a = 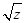 .
.
Программа проводит проверку на точность (eps) и останавливается, когда два последовательных приближения отличаются меньше чем на eps. При императивном подходе алгоритм обычно программируется следующим образом (на языке Си):
x = a0;
do{
y = x;
х = (х + z/x) / 2;
} while (abs(x-y) > eps)
// теперь x = квадратному корню из z
Предсавим эту программу в модульной форме, используя ленивые вычисления.
Так как алгоритм Ньютона-Рафсона вычисляет последовательность приближений, будем использовать для этого в программе список приближений. Каждое приближение получено из предыдущего с помощью функции
next zx =(x+z / x)/2
Данная функция, преобразует каждое текущее приближение в следующее. Обозначим эту функцию f, тогда последовательность приближений будет: [ а 0, f a 0, f (f a 0), f (f (f а 0)),...]. Определим функцию, вычисляющую данную последовательность:
iterate f х = х: iterate f (f x)
Тогда список приближений можно вычислить следующим образом:
iterate (next z) a 0
iterate это пример функции с «бесконечным» выводом. Однако фактически будет вычислено не больше приближений, чем требуется остальным частям программы. Таким образом, мы имеем потенциальную бесконечность.
Завершающая часть программы это функция within, которая использует оценку точности eps и список приближений. Она просматривает список и находит два последовательных приближения, отличающихся не более чем на eps.
within eps (a:b:rest) =
if abs(a-b) <= eps
then b
else within eps (b: rest)
Окончательно, получаем:
sqrt a 0 eps z = within eps (iterate (next z) a 0)
Мы можем объединять полученные части программы различными способами. Одна из модификаций заключается в использовании относительной погрешности вместо абсолютной. Она применима как для очень малых чисел (когда различие между последовательными приближениями маленькое), так и для очень больших (при округлении ошибки могут быть намного большими, чем eps). Заменим within функцией
relative eps (a:b:rest) =
if abs(a-b) <= eps*abs(b)
then b else
relative eps (b:rest)
Т.о. получим новую версию sqrt
relative sqrt a 0 eps z = relative eps (iterate (next z) a 0)
Нет необходимости переписывать часть, которая генерирует приближения.
Запишем алгоритм определения корня функции f методом касательных. Если начальное приближение равно x0, то следующее приближение вычисляется по формуле х 1 = х - f(x) / f '(x). На языке Haskell этот алгоритм можно представить следующим образом:
root f diff x0 eps = within eps (iterate (next f diff) x0)
where next f diff x = x - f x / diff x
Для работы этого алгоритма необходимо указать две функции: f, вычисляющню значение функции f и diff, вычисляющую значение f '. Например, чтобы найти положительный корень функции f(x) = х2 - 1с начальным приближением 2, составим следующее выражение:
root f diff 2 0.001 where f x = x^2 - 1
diff x = 2*x
 2014-02-13
2014-02-13 654
654







