2014-02-13
2855
И ФОРМАЛЬНЫЕ ЛОГИЧЕСКИЕ СИСТЕМЫ
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ЛОГИЧЕСКОГО ВЫВОДА
3.1. Понятие логического вывода. Типы логических рассуждений. Критерий правильности дедуктивных рассуждений.
3.2. Принципы построения формальных логических систем.
3.3. Исчисление высказываний (ИВ) - формальное определение, основные понятия, правила вывода, методы логического вывода (доказательства теорем) в ИВ:
с помощью "таблиц истинности", метод резолюции.
3.4. Исчисление предикатов (ИП): - формальное определение, основные понятия (атомарные формулы, термы, функции, кванторы), правила вывода, методы доказательства теорем в ИП: с помощью непосредственного применения правил вывода, метод резолюции.
3.1. Логический вывод (логические рассуждения)
- это процесс рассуждений, позволяющих от некоторых исходных утверждений, считающихся истинными (и называемых ПОСЫЛКАМИ или ГИПОТЕЗАМИ), перейти к новым утверждениям, логически вытекающим из исходных, т.е. к ЗАКЛЮЧЕНИЯМ.
Это один из основных подходов, используемых человеком при решении трудно формализуемых задач. Запись A1,.., An ½¾ B означает: "Если истинны A1,.., An, тоистинно B, т.е.из посылок A1,.., An логически следует заключение B ". Типы логических рассуждений:(а) дедуктивные – "от общего к частному" (посылки A1,.., An являются более общими, чем заключение B);(б) индуктивные – "от частного к общему" (посылки A1,.., An являются менее общими, чем заключение B); (в) традуктивные – "от частного к частному" (и посылки и заключение имеют одинаковую степень общности).
|
|
|
Дедуктивные рассуждения являются достоверными, т.е. от истинных посылок они всегда приводят только к истинному заключению.
Индуктивные и традуктивные рассуждения являются правдоподобными (гипотетическими), т.к. от истинных посылок они могут приводить как к истинному, так и к ложному заключению. Индуктивные заключения (обобщения) имеют ценность как средство поиска гипотез, но не как средство их подтверждения.
3.2. Принципы построения формальных логических систем.
Формальная логическая система (теория, исчисление) определена, если
- задан ЯЗЫК теории,т.е. алфавит (конечное множество символов) и синтаксис (набор правил построения последовательностей символов алфавита, т.е. предложений или правильно построенных формул - ППФ, часто называемых просто формулами);
- задано множество АКСИОМ теории, т.е. некоторое подмножество ППФ, которые приняты истинными в данной логической системе;
- задано конечное множество ПРАВИЛ ВЫВОДА, позволяющих получать заключения на основе посылок.
Вид правила вывода: F1,..,Fn / G, что означает: "Если истинны формулы F1,..,Fn, то истинна и формула G ".
|
|
|
3.3. Исчисление высказываний (ИВ)
Высказывание - этоутверждение, которое может быть либо истинным (И),либо ложным (Л) ине может быть тем и другим одновременно.
Определение исчисления высказываний (ИВ), как ФЛС:
1. ЯЗЫК ИВ:
(1) алфавит ИВ: ( а) символы элементарных или атомарных (т.е. неделимых)высказываний (пропозициональные переменные), которые могут принимать значения И или Л: a, b, c, d, …;( б) символы логических операций (логических или пропозициональных) связок: & или Ù - конъюнкция, Ú - дизъюнкция, Ø - отрицание, ® - импликация, « - эквивалентность; (в) () - символы скобок.
(2) синтаксис ИВ - правила построения ППФ:
- символ элементарного высказывания (пропозициональная переменная) есть
ППФ: a,b,...
- если P и Q - это ППФ, то выражения P & Q, P Ú Q, ØP, P ® Q, P «Q,
так же являются ППФ:
- других ППФ нет.
Большие буквы, используемые для сокращенного обозначения формул, не являются символами ИВ. Для операции импликации ("если А, то В") справедлива формула: P ® Q = ØP Ú Q.
2. АКСИОМЫ ИВ. Наиболее известны следующие системы аксиом ИВ:
(а). Система П.С. Новикова (11 аксиом, используются 4 связки &,Ú, Ø, ®);
(б). Система Б. Рассела и А.Н. Уайтхеда (4 аксиомы, используются 2 связки Ú, ®);
(в). Система Д. Гилберта (вариант) (4 аксиомы, используются 2 связки Ú, ®).
(г). Система, состоящая из 3 аксиом (используются 2 связки Ø, ®).
3. ПРАВИЛА ВЫВОДА в ИВ.
(1).ПРАВИЛО ПОДСТАНОВКИ: U(a) / U(В) - "Если истинно U(a), то истинно и U(В) ", т.е.если U(a) - истинная формула ИВ, содержащая переменную a, то истинной является и формула U(В), которая получается из U(a) заменой ВСЕХ вхождений переменной a на произвольную формулу В, не содержащую переменную a.
(2).ПРАВИЛО ЗАКЛЮЧЕНИЯ - Modus Ponens (Modus Ponendo Ponens):
A, (A ® B) / B: "Если А истинно и из А следует В, то и В истинно ".
Доказательство теорем в ИВ.
Даны: - ППФ А1,..., Аn - посылки (гипотезы);
- ППФ В - утверждение, называемое теоремой.
Требуется установить: истинно ли утверждение В, если истинны посылки А1,..., Аn. Если это так, то В является логическим следствием посылок А1,..., Аn (обозначение: А1,..., Аn |- В), т.е. теорема доказана; если это не так, то теорема опровергнута.. Существуют два подхода к доказательству теорем - семантический и синтаксический.
1. Семантический подход - д оказательство осуществляется на основе семантики (т.е. истинностных значений ППФ). Наиболее простой семантический метод - метод таблиц истинности: рассмотреть все возможные присваивания значений истинности (т.е. И или Л) элементарным высказываниям, входящим в посылки, и выявить такие наборы значений этих элементарных высказываний, которые делают истинными ВСЕ посылки. Теорема доказана тогда и только тогда, когда утверждение В истинно на всех этихнаборах.
Пример 1
Элементарные высказывания (переменные):
p – я читаю скучную книгу; q - мне хочется спать.
Посылки:
П1: p ® q "Если я читаю скучную книгу, то мне хочется спать"
П2: p "Сейчас я читаю скучную книгу "
Теорема: Т = q "Сейчас мне хочется спать" – доказать.
Таблица истинности Табл. 2
| p | q | П1: p ® q = = ` p Ú q | П2: p | Т: q |
Поскольку на наборе значений переменных p =1, q = 1, на котором истинны ВСЕ посылки, т.е. П1 и П 2, истинна так же и ППФ, представляющая теорему Т: q =1 то теорема доказана.
2. Синтаксический подход - д оказательство осуществляется путем формальных преобразований ППФ, представляющих посылки и теорему, с помощью правил вывода (без присвоения конкретных значений истинности элементарным высказываниям).
Один из эффективных методов - метод резолюции [1,2,4]. В его основе - принцип опровержения: предполагается, что теорема В при истинности посылок А1,..., Аn ложна. Тогда ее отрицание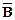 
истинно (при истинности посылок). Следовательно, для доказательства теоремы надо доказать, что данное предположение ложно, т.е. что ложно утверждение 
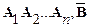. Это утверждение ложно в том случае, если одновременная истинность всех посылок А1,..., Аn и отрицания теоремы 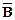приводит к противоречию, т.е. к такой ситуации, когда какая-либо из переменных, входящих в посылки или в отрицание теоремы, например p, и ее отрицание ` p ("не- p ") одновременно должны быть истинными. Если достигнута такая ситуация, то поскольку по закону противоречия в классической логике она невозможна, отрицание теоремы (при истинности посылок) ложно, а теорема истинна..
|
|
|
Ход доказательства: пытаемся (с помощью некоторой процедуры) доказать истинность утверждения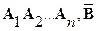 
,т.е. истинность отрицания теоремы при истинности всех посылок.. Если эта процедура приводит к противоречию, то значит, попытка неудачна, т.е. отрицание теоремы ложно, и, следовательно, теорема истинна, т.е. доказана. Указанная процедура выполняется с помощью специального правила вывода - правила резолюции, применяемого к посылкам и отрицанию теоремы, представленным в конъюнктивной форме (введено Дж. Робинсоном в 1965).
Термины: литерал (литера) - это пропозициональная переменная (элементарное высказывание) или ее отрицание: a, b, `c, `r, …; дизъюнкт (clause) – это дизъюнкция конечного числа литералов (напр., (a Ú b Ú `c); ( `e Ú x); d; `y); конъюнктивная форма высказывания – это конъюнкцияконечного числа дизъюнктов, например:
A = (a Ú b Ú` c) &`(e Ú x) & d & y = (a Ú b Ú `c)`(e Ú x) d y.
ПРАВИЛО РЕЗОЛЮЦИИ. Если два дизъюнкта имеют вид: M = (a Ú Y) и N = (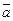 
Ú Z),
(где a и ` 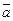- литералы, а Y, Z - некоторые дизъюнкции литералов, то справедливо
(a Ú Y) ( 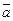Ú Z) ® (Y Ú Z).
Применение этого правила к дизъюнктам (a Ú Y) и ( 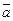Ú Z) называется резолюцией этих дизъюнктов, предложение (Y Ú Z) - их резольвентой, а литералы вида a и 
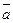- называются контрарными друг другу (контрарной парой). Например, если Y= b Ú 
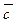Ú e; Z = d Ú `m Ú r, то резольвента R =(Y Ú Z) = (b Ú 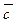Ú e Ú d Ú `m Ú r).
|
|
|
ПРОЦЕДУРА ДОКАЗАТЕЛЬСТВА ТЕОРЕМ в ИВ МЕТОДОМ
РЕЗОЛЮЦИИ
1. Представить каждую из посылок и отрицание теоремы в конъюнктивной форме (т.е. как конъюнкцию или множество дизъюнктов).
2. Сформировать множество G, включающее все полученные дизъюнкты, являющиеся членами как посылок, так и отрицания теоремы (которое может быть представлено как конъюнкция ВСЕХ полученных дизъюнктов).
3. Найти в этом множестве два любых дизъюнкта, содержащих контрарную пару литералов x и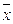 
(т.е. таких, что если один из них содержит какую-либо переменную x, то другой содержит ).
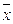4. Выполнить резолюцию этих двух дизъюнктов и получить резольвенту R.
5. Включить резольвенту в исходное множество дизъюнктов, т.е. в Г, удалив из него дизъюнкты, подвергшиеся резолюции, и продолжить процесс до тех пор, пока не произойдет одно из двух событий:
(1) возникнет противоречие по отношению к какой-либо переменной (например, p и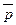 
одновременно должны быть истинными); это значит, что отрицание теоремы не является истинным при истинности посылок, т.е. оно ложно, а следовательно, теорема истинна, т.е. доказана.
(2) возникнет ситуация, когда в множестве G нет дизъюнктов, над которыми можно произвести резолюцию, т.е. невозможно построение новых предложений, а противоречие не встретилось. Это значит, что при истинности посылок отрицание теоремы истинно, а следовательно, теорема ложна, т.е. не доказана (опровергается).
3.4. Исчисление предикатов (ИП)
Эта ФЛС включает все исчисление высказываний (ИВ), т.е. элементарные высказывания, все операции ИВ, и все формулы ИВ, но помимо этого ИП рассматривает утверждения, которые расчленяются на субъект и предикат, где субъект – логическое подлежащее, т.е. предмет суждения (предмет, факт, явление, процесс и т.д.), предикат - логическое сказуемое, т.е. то, что в утверждении высказывается о подлежащем. Например: "Отец Васи – инженер". Отец Васи - субъект, инженер - предикат.
Субъекты – это либо константы, т.е. конкретные предметы, явления, факты и т.д., названные определенными именами, либо переменные, определяющие класс или множество субъектов. Предикат отражает некоторые свойства субъекта или отношения между субъектами какой-либо группы, т.е. описывает некоторую связь, заданную на множестве констант или переменных.
Такие утверждения могут быть как ИСТИННЫМИ, так и ЛОЖНЫМИ.
Определение. Двузначный предикатэто логическая функция от некоторого числа аргументов, которая принимает одно из двух возможных значений – ИСТИНА (И) или ЛОЖЬ (Л), тогда как значениями ее аргументов могут быть элементы произвольных заданных множеств.
Предикат - это неоднороднаялогическая функция в отличие от функций ИВ, которые называются однородными, посколькукак сами функции ИВ, так и их аргументы принимают значения из одного и того же множества { И, Л }.
Предикат, число аргументов которого равно n, называется n -местным и обозначается P(x1,x2,…, xn), где x1,x2,…, xn - аргументы предиката, называемые предметными или индивидуальными переменными. Они обозначают произвольные элементы заданных множеств M1, M2,..., Mn, т.е. x1 Î M1,.., xn Î Mn Множество Mi - это область определения предметной переменной x i (i=1,…,n).
Множество M = M1 ´ M2 ´... Mn, т.е. декартово произведение областей определения аргументов x1, x2,…, xn, содержит все возможные упорядоченные наборы значений аргументов длины n и называется полем предиката P(x1,x2,…, xn) или универсумом.
Одноместный предикат выражает свойство субъекта (единственного), n -местный предикат при n >1 выражает отношения между n субъектами, соответствующими его аргументам.
Основные понятия
Важнейшие понятия в ИП - понятия ФУНКЦИИ и ОТНОШЕНИЯ [10,11].
ФУНКЦИЯ f (x1, x2 ,.., xk) от k аргументов задает отображение k элементов изобласти определения этих аргументовна ОДИН элемент ИЗ ЭТОЙ ЖЕ ОБЛАСТИ [11], иначе говоря, "функция есть отображение, которое отображает список констант в данную константу "[10]. Символ f (x1, x2 ,.., xk), используемый для обозначения функции от k аргументов, называется k-местным функциональным символом.. В качестве таких символов обычно используются буквы f, g, h, j, y, g,… или некоторые слова и словосочетания, связанные со смыслом данной функции.
Примеры.
1.Область определения аргументов - множество рациональных чисел. Выражение z = произведение(x, y), описывающее функцию произведения двух чисел, означает, что число z есть произведение чисел x и y, т.е.отображает два натуральных числа x и y на одно натуральное число z. При x =3, y =5 получим z =15.
2. Область определения - множество людей. Пусть отец(x) – функция "быть отцом", т.е. запись y = отец (x) - означает, что y - это ЧЕЛОВЕК, который является отцом любого человека, представленного переменной x. Пусть отцом конкретного человека по имени Николай, является Василий. Это значит, что если x =Николай, то y = отец(Николай)=Василий.
Функцию отец (x) можно обозначить f (x), тогда выражение " y является отцом x" запишется как y= f(x), выражение "r является дедушкой x" - как r = f (f (x)), т.е. r – отец отца x, выражение "Василий - отец Николая" как - Василий = f (Николай), а если дедушкой Николая является Степан, то r = f (f (Николай)) = Степан.
ОТНОШЕНИЕ (k-местное) - это отображение k элементов изданной области определения аргументовна элемент множества {ИСТНА, ЛОЖЬ}={ И, Л }.
Примеры.
1.Область определения - множество рациональных чисел.
(а).Введем ОТНОШЕНИЕ: ПРОИЗВЕДЕНИЕ ( x, y, z), которое означает " z является произведением чисел x и y ". Это высказывание может принять одно из двух значений: И или Л. Так ПРОИЗВЕДЕНИЕ (2, 3, 6) = ИСТИНА, ПРОИЗВЕДЕНИЕ (2, 3, 8) = ЛОЖЬ.
(б).ОТНОШЕНИЕ: БОЛЬШЕ ( x, y) - "x больше y".
Тогда БОЛЬШЕ (7, 9) = Л, БОЛЬШЕ (5, 2) = И.
(в). Используя понятия функции и отношения предложение "(x ´ y) больше, чем y" можно представить в виде БОЛЬШЕ ( произведение(x, y),y ).
Тогда БОЛЬШЕ ( произведение(2, 4),4 ) = И, БОЛЬШЕ ( произведение(0.5, 4),4 ) =Л.
2.Область определения - множество людей. Введем ОТНОШЕНИЕ: ОТЕЦ(у,x) – " у является отцом x". Если в реальности отцом конкретного человека по имени Николай, является Василий, то это отношение может иметь следующие значения: ОТЕЦ(Василий,Николай)= И, ОТЕЦ(Андрей,Николай)= Л.
В ИПэлементарным объектом, принимающим значение ИСТИНА или ЛОЖЬ, является АТОМАРНАЯ ФОРМУЛА (АТОМ), котораяимеет вид P (t1, t2,…, tn),где t1, t2,…, tn - аргументы предиката, называемые ТЕРМАМИ; P – предикатный символ,т.е. имя отношения, существующего между аргументами, или имя свойства, если аргумент один. ТЕРМ – определяется индуктивно:
1. Любая КОНСТАНТА и любая ПРЕДМЕТНАЯ ПЕРЕМЕННАЯ - ТЕРМЫ.
2. Если f – n -местный функциональный символ, а t1, t2,…, tn – ТЕРМЫ, то выражение f(t1, t2,…, tn) – является ТЕРМОМ.
3. Других термов нет.
Термы вида f(t1, t2,…, tn) называются составными термами или структурами.
Примеры термов: x (переменная); 7, С (константы); j (x, y); сумма (х, 5); произведение (х, сумма (z,5)), брат (у), брат (отец (Петр)) - составные термы.
Примеры НЕ термов: j (f); 100(Ú, z); y(d, C) &.
Атомарная формула и ее отрицание называются ЛИТЕРАЛАМИ.
КВАНТОРЫ
Значение предикатного выражения (ИСТИНА или ЛОЖЬ) зависит от значений входящих в него предметных переменных. Если этим переменным не присвоены конкретные значения, то значение предикатного выражения (атомарной формулы) не определено.
Для того, чтобы атомарной формуле можно было присваивать определенные значения истинности, не перебирая ВСЕ возможные значения предметных переменных, вводятся два специальных оператора, называемые КВАНТОРАМИ, которые позволяют задать значения предикатного выражения для двух крайних случаев.
1. Факт, описанный предикатным выражением P( x,y.., B,C,..), имеет место при ВСЕХ значениях данной переменной xÎ X, где X - ее область определения, т.е. формула P( x,y.., B,C,..) ИСТИННА при любом значении переменной x из ее области определения (независимо от значений всех других переменных). Это записывается как " x P(x, y,.., B,C,..) - "Для всех xÎ X справедливо P(x, y,.., B,C,..) ". Символ " x называется КВАНТОРОМ ОБЩНОСТИ (ВСЕОБЩНОСТИ).
2. Факт, описанный предикатным выражением P(x, y,.., B,C,..), имеет место для НЕКОТОРЫХ значений переменной x (хотя эти значения могут быть и неизвестны), т.е. в области определения переменной x имеются такие ее значения (хотя бы одно), при которыхформула P(x, y,.., B,C,..) ИСТИННА. Это записывается как: $x P(x, y,.., B,C,..) - "Существуют такие значения xÎ X, для которыхсправедливо P(x, y,.., B,C,..) ". Символ $ x называется КВАНТОРОМ СУЩЕСТВОВАНИЯ.
Переменная, к которой применен квантор, называется связанной, остальные переменные – свободными. Применение кванторов к каким-либо переменным называется квантификацией переменных.
Примеры
1. Рассмотрим предикатное выражение ЗНАТЬ_ЯЗЫК (x, y),
где x ÎX, X - множество московских студентов, y ÎY, Y - множество европейских языков, т.е. "Студент x знает язык y ".
Пусть y = Фр(франц. яз.), тогда, очевидно: (а) "x ЗНАТЬ_ЯЗЫК (x, Фр) = ЛОЖЬ ("Все московские студенты знают французский язык"- ЛОЖЬ, т.к. я знаю нескольких студентов, незнающих этот язык); (б) $x ЗНАТЬ_ЯЗЫК (x, Фр) = ИСТИНА ("Есть хотя бы один московский студент, который знает французский язык", и я знаю этого студента).
2. Пусть есть предикатное выражение БОЛЬШЕ ( y,x ) - " y больше x". Тогдаутверждение "Для каждого числа x существует число y, которое больше, чем x " можно представить как " x $ y БОЛЬШЕ ( y,x ).
Формальное определение ИП [12]:
I. ЯЗЫК ИП
- АЛФАВИТ ИП:
- предметные (индивидуальные) переменные: w, v, x, y …или x1, x2…
- предметные константы (имена объектов): A, B, C, …
- функциональные символы: f1, f2 ,…j, y..
- предикатные символы: P1, P2,.. Pm, Q, R,…
- символы кванторов: ", $
- алфавит исчисления высказываний (ИВ):
(а) пропозициональные (логические) переменные a, b, c, d…, принимающие
значения И или Л; (в) логические связки Ú, &, Ø, ® и скобки ().
- СИНТАКСИС ИП - правила построения ППФ:
1. Атомарная формула P(t1, t2,…, tn) - есть ППФ.
2. Если R и Q являются ППФ, то следующие выражения, построенные из R и Q с помощью связок ИВ, так же являются ППФ:
ØR, R Ú Q, R & Q, R ® Q
3. Если R (x,…) – это ППФ, содержащая свободную переменную x, то выражения "xR (x,…) и $ x R (x,…) также являются ППФ.
4. Других ППФ нет.
II. АКСИОМЫ ИП
В качестве аксиом ИП принимается любая система аксиом ИВ, к которой добавляются две следующих аксиомы
(а) "x P(x) ® P(y)
(б) P(y) ® $x P(x)
III. ПРАВИЛА ВЫВОДА
1. Правило заключения (Modus Ponens)
