P , P ® Q

Q, где P и Q - произвольные ППФ исчисления предикатов.

2. Правило специализации

" x P(x, y,z, …)

P(А, y,z, …),

т.е. если истинна формула "x P(x, y,z, …), где x – переменная из некоторой области определения, то истинна и формула P(А, y,z, …), где А - любая константа (имя предмета из данной области определения).

ДОКАЗАТЕЛЬСТВО ТЕОРЕМ В ИП.

1. Прямое доказательство - последовательное применение правил вывода, начиная с аксиом. Применяемые правила вывода должны быть логичными.

Правила вывода, составляющие некоторое множество, называют логичными, если те ППФ (теоремы), истинность которых при условии истинности посылок может быть установлена с помощью этих правил, ДЕЙСТВИТЕЛЬНО логически следуют из данного множества посылок (что может быть установлено некоторым другим способом, например, с помощью таблиц истинности) [5].

Основными применяемыми при доказательстве правилами вывода являются правило заключения (Modus Ponens) и правило специализации (см. выше), которые являются логичными.

Правило специализации позволяет освободиться от квантора общности ", что бывает необходимо для последующего выполнения правила заключения, поэтому оно обычно применяется до выполнения правила заключения (часто уже на первом шаге доказательства).

Пример 1

Пусть есть два предиката:

ИМЕТЬ_ПОЦЕССОР( x ) - "объект x имеет процессор "

КОМПЬЮТЕР(x) - "объект x является компьютером",

где x Î X, X – множество материальных тел.

ПОСЫЛКИ

(1) ИМЕТЬ_ ПРОЦЕССОР (WEST)	"Объект с именем WESTимеет процессор"
(2)" x ИМЕТЬ_ПРОЦЕССОР(x)® КОМПЬЮТЕР(x)	"Для всех x справедливо: если x имеет процессор, то x является компьютером* "*
................................................................................................. Теорема (доказать): КОМПЬЮТЕР (WEST)	............................................ "Объект WEST является компьютером "

1. Применяем правило специализации к посылке

(2) " x ИМЕТЬ_ПРОЦЕССОР( x )® КОМПЬЮТЕР(x), считая, что

P(x) = ИМЕТЬ_ПРОЦЕССОР (x)® КОМПЬЮТЕР(x) и положив x = WEST.

Получим выражение

(2а). ИМЕТЬ_ПРОЦЕССОР( WEST )® КОМПЬЮТЕР( WEST )

2. Применяем правило заключения R, R ® S к выражениям (1) и (2а):

S

(1) R: ИМЕТЬ_ПРОЦЕССОР( WEST )

(2а) R ® S: ИМЕТЬ_ПРОЦЕССОР( WEST )® КОМПЬЮТЕР( WEST )

Получим: утверждение S = КОМПЬЮТЕР( WEST ) - истинно.

Теорема доказана.

2. Доказательство с помощью правила резолюции [5].

Схема доказательства аналогична применяемой в ИВ (см. выше).

В попытке доказать истинность отрицания теоремы правило резолюции (LÚ Y) ( 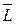Ú Z) ® (Y Ú Z) применяется к парам ППФ, имеющим вид дизъюнктов. ( LÚ Y) и ( 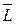Ú Z), где L и ` 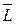- литералы, а Y, Z - некоторые дизъюнкции литералов.

Для выполнения процедуры доказательства все ППФ, описывающие посылки и отрицание теоремы, должны быть представлены в конъюнктивной форме (т.е. как конъюнкции или множества дизъюнктов). Показано, что любая ППФ исчисления предикатов может быть преобразована в такую форму и процесс преобразования описан в [5]. Поскольку в ИП литералами являются атомарные формулы и их отрицания, в общем случае содержащие кванторы, то процесс указанного преобразования, включающий освобождение от кванторов, является достаточно сложным, особенно в связи с исключением квантора существования. Поэтому далее рассмотрим случай, требующий исключения только квантора общности.

Пример 2. Пусть требуется доказать теорему, сформулированную в Примере 1.

Применив правило специализации к посылке (2), получим представление этой посылки в виде выражения (2а), затем преобразуем это выражение в конъюнктивную форму, исключив операцию импликациив соответствии с формулой P®Q =` P Ú Q.

Получим:

(2а)ИМЕТЬ_ПРОЦЕССОР( WEST ) ® КОМПЬЮТЕР( WEST ) =

= ИМЕТЬ_ПРОЦЕССОР( WEST ) V КОМПЬЮТЕР( WEST )

Далее выполним описанную выше процедуру доказательства:

(1) ИМЕТЬ_ ПРОЦЕССОР ( WEST )

КОМПЬЮТЕР ( WEST )

(2а) ИМЕТЬ_ПРОЦЕССОР( WEST ) V

V КОМПЬЮТЕР ( WEST)

(3) `T: КОМПЬЮТЕР ( WEST ) Ä противоречие

Получено ПРОТИВОРЕЧИЕ, следовательно, теорема доказана.