Таблица 4.1
| Источник рассеяния | Сумма квадратов отклонений | Число степеней свободы | Оценка дисперсии |
| Относительно линии регрессии | 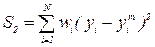 | N-(k+1) | 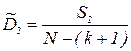 |
| За счет регрессии | 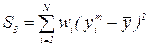 | (k+1)-1 | 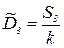 |
| Общее отклонение | 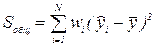 | N-1 | 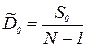 |
Так как оценка дисперсии Di "характеризующая чистую ошибку (дисперсия воспроизводимости) в таблице отсутствует, то для получения оценки дисперсии ошибки наблюдений 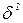 в одной из точек проводится несколько (n) повторных наблюдений и в качестве оценки дисперсии ошибки наблюдений используют
в одной из точек проводится несколько (n) повторных наблюдений и в качестве оценки дисперсии ошибки наблюдений используют
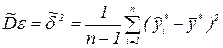
где 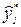 1-е наблюдение в выбранной точке (обычно наблюдения проводят в центре плана),
1-е наблюдение в выбранной точке (обычно наблюдения проводят в центре плана), 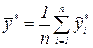 - среднее значение.
- среднее значение.
Если в каждой точке хi проводится по ni наблюдений, то в качестве оценки дисперсии ошибки наблюдений 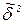 можно использовать величину
можно использовать величину
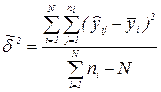 , где
, где 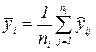
В качестве весовых коэффициентов используются значения wi = ni.
Знание оценки дисперсии ошибки 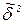 позволяет провести анализ, качества уравнения регрессии.
позволяет провести анализ, качества уравнения регрессии.
Примем, как и ранее, гипотезу о нормальном законе распределения ошибки с 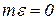 и
и 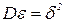 . Для проверки адекватности уравнения регрессии проверим гипотезу Н0, состоящую в том, что
. Для проверки адекватности уравнения регрессии проверим гипотезу Н0, состоящую в том, что 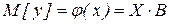 (Н0: Dад = Dвос). т.е. уравнение регрессии
(Н0: Dад = Dвос). т.е. уравнение регрессии 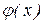 хорошо описывает результаты наблюдений, против альтернативной гипотезы H1:
хорошо описывает результаты наблюдений, против альтернативной гипотезы H1: 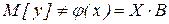 .
.
В качестве меры рассогласования будем использовать дисперсионное отношение вида 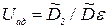 . Эта величина подчинена F - распределению с числом степеней свободы (N - (k+1) - числителя и (п-1) - знаменателя. Если при заданном уровне значимости а вычисленное значение Uад меньше UKp (UKp - из таблицы F-распределения), то модель адекватна. Иначе (Uад>Uкр) модель неадекватна. Если модель адекватна, то в качестве оценки дисперсии ошибки можно использовать либо оценку
. Эта величина подчинена F - распределению с числом степеней свободы (N - (k+1) - числителя и (п-1) - знаменателя. Если при заданном уровне значимости а вычисленное значение Uад меньше UKp (UKp - из таблицы F-распределения), то модель адекватна. Иначе (Uад>Uкр) модель неадекватна. Если модель адекватна, то в качестве оценки дисперсии ошибки можно использовать либо оценку 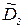 . т.е.
. т.е. 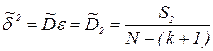
где S2 подчинена 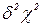 - распределению с числом степеней свободы
- распределению с числом степеней свободы
г = N-(k+l), либо величину 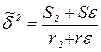 , где г2 = N-(k+l);
, где г2 = N-(k+l); 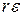 =n - 1. Здесь
=n - 1. Здесь  подчинена
подчинена 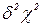 - распределению с числом степеней свободы
- распределению с числом степеней свободы 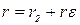
В случае адекватности найденного уравнения регрессии можно проверить значимость отдельных его коэффициентов bi i=0,1,...,k.
В общем случае при произвольном плане экспериментов коэффициенты линии регрессии являются зависимыми случайными величинами. Поэтому доверительная область (область, в которой действительные значения коэффициентов регрессии находятся с заданной вероятностью 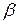 ) представляет собой эллипсоид в (k+1)-мерном пространстве с центром в точке
) представляет собой эллипсоид в (k+1)-мерном пространстве с центром в точке 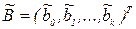 . Положение доверительного интервала для каждого из коэффициентов bi зависит от заданных значений остальных bj,
. Положение доверительного интервала для каждого из коэффициентов bi зависит от заданных значений остальных bj, 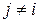 . Границы эллипсоида задаются неравенством
. Границы эллипсоида задаются неравенством
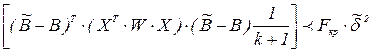
Значение FKp берется из F-распределения для заданного уровня значимости 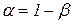 при числе степеней свободы числителя rч=(k+1) и гзн знаменателя, которое принимается равным N - (k+1) или
при числе степеней свободы числителя rч=(k+1) и гзн знаменателя, которое принимается равным N - (k+1) или 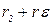 , в зависимости от того, какое соотношение используется для вычисления оценки
, в зависимости от того, какое соотношение используется для вычисления оценки 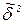 (см. п.4.3).
(см. п.4.3).
Проверка значимости коэффициентов заключается в проверке гипотезы Н0: В=Взад= (0. 0..... 0)т. Если при этом неравенство выполняется, то все коэффициенты незначимы. В противном случае все коэффициенты или часть из них значимы и проверять их значимость нужно по отдельности, задавая значения 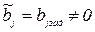 остальным коэффициентам.
остальным коэффициентам.
Если при проведении экспериментов план эксперимента был ортогональным, то оценки коэффициентов регрессии независимы и проверку их значимости можно проводить независимо друг от друга.
При проверке значимости коэффициента bi проверяется гипотеза H01: bi=0. В качестве меры рассогласования используется статистика 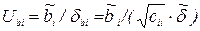 , которая подчинена t-распределению с числом степеней свободы г равным числу степеней свободы оценки дисперсии
, которая подчинена t-распределению с числом степеней свободы г равным числу степеней свободы оценки дисперсии 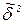 .
.
Если вычисленное значение U1 не превышает UKp, взятого из t-распределения при заданном уровне значимости 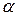 и числе степеней свободы г, то гипотеза Н0 принимается (коэффициент bi. незначим), в противном случае (Ui > UKp) коэффициент bi значим.
и числе степеней свободы г, то гипотеза Н0 принимается (коэффициент bi. незначим), в противном случае (Ui > UKp) коэффициент bi значим.
Если часть коэффициентов незначима, то их можно принять равными нулю. В этом случае необходимо снова проверить адекватность скорректированной модели. Если она окажется неадекватной, то исключать соответствующие переменные из нее нельзя.
4.5. Построение доверительного интервала для уравнения регрессии
Если модель адекватна и все коэффициенты регрессии значимы, то можно построить доверительный интервал для значений функции отклика, вычисляемых по уравнению регрессии.
Пусть 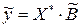 , где
, где 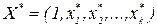 - значения входных переменных, при которых вычисляется значение выходной переменной по уравнению регрессии. Так как коэффициенты регрессии несмещенные, то и у также несмещенная случайная величина для которой
- значения входных переменных, при которых вычисляется значение выходной переменной по уравнению регрессии. Так как коэффициенты регрессии несмещенные, то и у также несмещенная случайная величина для которой 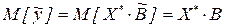 .
.
Так как 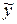 - линейная функция от коэффициентов В, которые, в свою очередь, линейные функции от нормально распределенных случайных величин
- линейная функция от коэффициентов В, которые, в свою очередь, линейные функции от нормально распределенных случайных величин 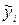 , то и у - нормально распределенная случайная величина, дисперсия которой равна
, то и у - нормально распределенная случайная величина, дисперсия которой равна
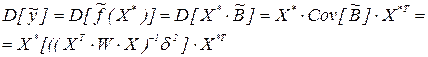
Отсюда доверительный интервал для значения у, вычисленного по уравнению регрессии будет 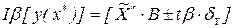 , где
, где 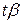 берется из t - распределения Стьюдента при числе степеней свободы оценки дисперсии ошибки
берется из t - распределения Стьюдента при числе степеней свободы оценки дисперсии ошибки 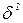 , используемой при вычислении
, используемой при вычислении 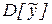 .
.
 2014-02-13
2014-02-13 806
806








