Таблица 3.2
| Источник рассеивания | Сумма квадратов отклонений | Число степеней свободы | Оценка дисперсии |
| 1. Чистая ошибка | 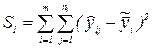 | 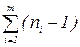 | 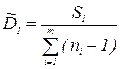 |
| 2. Отклонение относительно лини регресси | 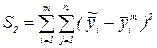 | (m-2) | 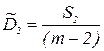 |
| 3. Отклонение засчет регрессии | 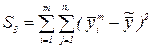 | 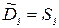 | |
| 4. Общее отклонение | 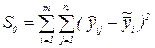 | 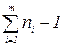 | 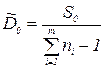 |
Вычисленные оценки дисперсий могут использоваться как для определения оценки дисперсии шума 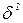 , так и для проведения анализа качества уравнения регрессии.
, так и для проведения анализа качества уравнения регрессии.
При этом дисперсия D1 часто называется дисперсией воспроизводимости, a D2 - дисперсией адекватности.
Для проведения анализа воспользуемся следующей теоремой разложения для 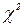 - распределения [6]:
- распределения [6]:
Пусть сумма Q, состоящая из N квадратов независимых нормально распределенных случайных величин xi с mxi = 0. 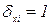 , разбита на m сумм квадратов нормально распределенных случайных величин Q1, Q2,..., Qm соответственно с r1,г2,..., rm степенями свободы:
, разбита на m сумм квадратов нормально распределенных случайных величин Q1, Q2,..., Qm соответственно с r1,г2,..., rm степенями свободы:
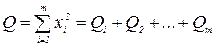
Тогда, если выполняется условие N = r1 + г2 +... + rm, то случайные величины Q1,Q2,..., Qm будут независимыми и распределенными по закону распределения 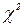 с числом степеней свободы соответственно r1, г2,..., rm.
с числом степеней свободы соответственно r1, г2,..., rm.
Так как в нашем случае значения выходной переменной у подчинены нормальному закону распределения и выполняется условие r0 = r1+г2+г3, то с учетом сделанных ранее допущений можно показать, что соответствующие вариации Sобщ, S1, S2 и S3 подчинены 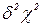 - распределению с числом степеней свободы соответственно r0, r1, r2 и г3.
- распределению с числом степеней свободы соответственно r0, r1, r2 и г3.
Кроме того, величина 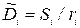 может использоваться как оценка дисперсии шума
может использоваться как оценка дисперсии шума 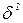 , так как
, так как 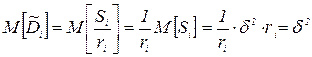 т е
т е 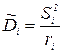
При этом на точность оценки 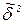 не влияет качество найденного уравнения регрессии
не влияет качество найденного уравнения регрессии 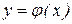 .
.
3.3. Проверка адекватности модели
Под адекватностью модели будем понимать то, что она хорошо (в статистическом смысле) описывает результаты наблюдений. Проверка адекватности заключается в оценке того, насколько хорошо значения 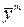 , вычисленные по найденному уравнению регрессии, согласуются со средними значениями переменной
, вычисленные по найденному уравнению регрессии, согласуются со средними значениями переменной 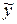 , найденными в результате наблюдений.
, найденными в результате наблюдений.
Рассмотрим гипотезу Н0, состоящую в том, что 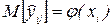 , где
, где 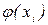 - найденное уравнение регрессии, против альтернативной гипотезы H1:
- найденное уравнение регрессии, против альтернативной гипотезы H1: 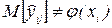 .
.
При переходе к усредненным по уровням переменной xi значениям наблюдаемой переменной получим для гипотезы Н0 эквивалентное условие: 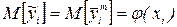 .
.
Рассеивание относительно этих математических ожиданий выходной переменной характеризуется дисперсиями воспроизводимости 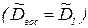 и адекватности
и адекватности 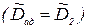 . Эквивалентной гипотезой будет Н'0: Dвос=Dад. В качестве меры рассогласования этих значений будем использовать дисперсионное отношение вида
. Эквивалентной гипотезой будет Н'0: Dвос=Dад. В качестве меры рассогласования этих значений будем использовать дисперсионное отношение вида 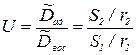
Так как вариации S2 и S1 подчинены 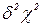 - распределению с числом степеней свободы г1 и г2 соответственно, то мера U подчинена F-распределению, с числом г2 степеней свободы числителя и r1 - знаменателя. Для величин D1 и D2 всегда выполняется соотношение D2>D1. Если при заданном уровне значимости
- распределению с числом степеней свободы г1 и г2 соответственно, то мера U подчинена F-распределению, с числом г2 степеней свободы числителя и r1 - знаменателя. Для величин D1 и D2 всегда выполняется соотношение D2>D1. Если при заданном уровне значимости 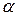 и степенях свободы г2 и r1 значение U, вычисленное по статистике, больше Uкр, взятого из таблицы (т.е. дисперсия Dад за счет отклонения найденного уравнения регрессии от действительного будет значимо больше дисперсии Dвос), то расхождение дисперсий (и соответственно средних) считается значимым и гипотеза Н0 отвергается. Модель считается неадекватной. В противном случае (U < UKp) нет оснований отвергнуть гипотезу Н0. Модель адекватна.
и степенях свободы г2 и r1 значение U, вычисленное по статистике, больше Uкр, взятого из таблицы (т.е. дисперсия Dад за счет отклонения найденного уравнения регрессии от действительного будет значимо больше дисперсии Dвос), то расхождение дисперсий (и соответственно средних) считается значимым и гипотеза Н0 отвергается. Модель считается неадекватной. В противном случае (U < UKp) нет оснований отвергнуть гипотезу Н0. Модель адекватна.
Если уравнение регрессии, найденное по результатам наблюдений, адекватно, то для получения более точной оценки дисперсии ошибки наблюдений 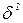 целесообразно использовать одновременно вариации S1 и S2, т.е.
целесообразно использовать одновременно вариации S1 и S2, т.е.
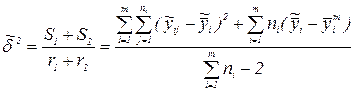
3.4. Проверка значимости коэффициентов регрессии
Для проверки значимости коэффициентов регрессии необходимо найти закон распределения оценок и его параметры - математическое ожидание и дисперсию.
Так как оценки параметров 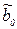 и
и 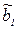
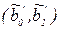 представляют собой линейные функции от случайной величины
представляют собой линейные функции от случайной величины 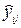 , распределенной по нормальному закону (см. допущения), то и оценки коэффициентов регрессии, найденные по МНК, будут распределены по нормальному закону с параметрами:
, распределенной по нормальному закону (см. допущения), то и оценки коэффициентов регрессии, найденные по МНК, будут распределены по нормальному закону с параметрами:
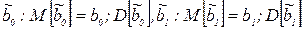
Дисперсии оценок могут быть найдены для случая уравнения регрессии
(3.3) достаточно просто:
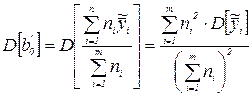
Так как 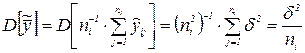 , то
, то
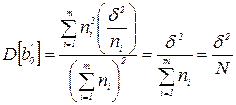
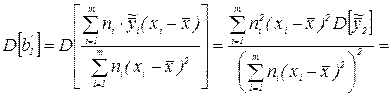
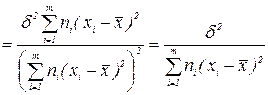
Для проверки значимости коэффициентов регрессии 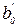 и
и 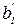 необходимо проверить гипотезы:
необходимо проверить гипотезы:
- для 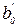 Н0:
Н0: 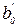 = 0 против альтернативы
= 0 против альтернативы 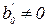 ;
;
- для 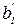 Н0:
Н0: 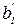 = 0 против альтернативы
= 0 против альтернативы 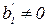 .
.
При проверке гипотез используются статистики вида
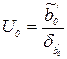 для
для 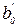 и
и 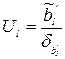 для
для 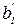 .
.
Поскольку точное значение 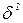 - неизвестно, то берется ее
- неизвестно, то берется ее
оценка 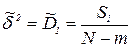 , где S1 имеет распределение
, где S1 имеет распределение 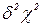 с
с
числом степеней свободы г =N - m. Отсюда статистики U0 и U1 подчинены t-распределению с числом степеней свободы соответственно
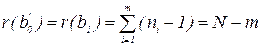
Доверительный интервал при уровне значимости 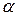 для них будет
для них будет 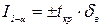 где
где 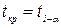 берется из распределению Стьюдента. Критическая область симметричная двухсторонняя.
берется из распределению Стьюдента. Критическая область симметричная двухсторонняя.
Если доверительный интервал накрывает начало координат, то коэффициент считается незначимым, в противном случае - значимым.
Так, при проверке гипотезы H0: 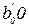 ,
, 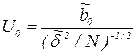 . Если
. Если 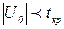 , то
, то 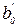 - незначим, иначе - значим. При проверке гипотезы Н0:
- незначим, иначе - значим. При проверке гипотезы Н0: 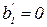 вычисляется статистика
вычисляется статистика 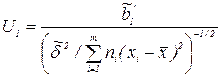
Если |U1 | < tKp, то b1 - незначим.
Если коэффициенты 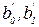 (или какой-либо из них) незначимы, то их в уравнении регрессии можно не учитывать. Если тот или иной член исключается из уравнения регрессии из-за незначимости соответствующего коэффициента, то необходимо заново пересчитать оценку дисперсии адекватности, изменив вид уравнения регрессии. Очевидно, что при этом могут измениться выводы относительно адекватности самой модели.
(или какой-либо из них) незначимы, то их в уравнении регрессии можно не учитывать. Если тот или иной член исключается из уравнения регрессии из-за незначимости соответствующего коэффициента, то необходимо заново пересчитать оценку дисперсии адекватности, изменив вид уравнения регрессии. Очевидно, что при этом могут измениться выводы относительно адекватности самой модели.
Аналогично определяется значимость коэффициентов b0 и b1 уравнения регрессии вида (3.1).
Так как 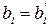 , то
, то
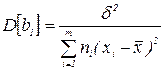
Учитывая, что 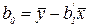 , можно показать, что
, можно показать, что
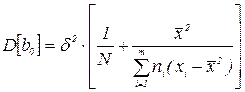
Вместо 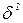 берется ее оценка
берется ее оценка 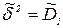 . Однако необходимо иметь в виду, что получаемые оценки b0 и b1 зависимы и для проверки их значимости необходимо строить эллипсоид рассеивания (рис. 3.2).
. Однако необходимо иметь в виду, что получаемые оценки b0 и b1 зависимы и для проверки их значимости необходимо строить эллипсоид рассеивания (рис. 3.2).
При построении доверительного интервала для одного из коэффициентов (например, для b1) необходимо задавать значение другого коэффициента (b0*).

Рис. 3.2
В остальном проверка значимости коэффициентов b0 и b1 аналогична проверке значимости коэффициентов 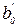 и
и 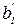 .
.
Доверительный интервал может быть построен и для значений переменной у, вычисляемой с помощью найденного уравнения регрессии в заданной точке х = х0. Так, для уравнения вила (3.2) математическое ожидание оценки у будет
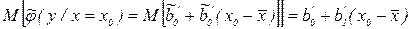 , а дисперсия оценки
, а дисперсия оценки
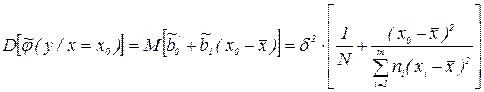
Доверительный интервал 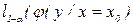 будет
будет
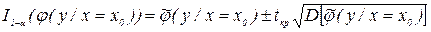
Вместо 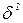 берется ее оценка
берется ее оценка 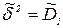 . Значение tKp берется из t-распределения с числом степеней свободы соответственно г = N-m.
. Значение tKp берется из t-распределения с числом степеней свободы соответственно г = N-m.
Если используется уравнение вида (3.1): 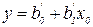 , то
, то 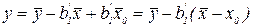 , отсюда
, отсюда
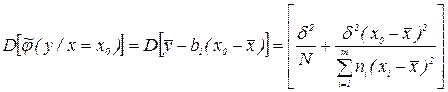
т.е. совпадает со значением, полученным для уравнения (3.2). Доверительный интервал 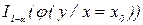 также не изменяется.
также не изменяется.
Будем рассматривать прежние результаты наблюдений (см. табл.3.1). Однако, прежде чем переходить к определению коэффициентов регрессии b0 и b1 проведем предварительную их обработку.
Представим результаты наблюдений в каждой точке xi в виде
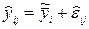 , где, как и ранее
, где, как и ранее 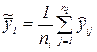 ,
, 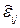 – случайная величина, характеризующая отклонение результатов наблюдений от среднего значения
– случайная величина, характеризующая отклонение результатов наблюдений от среднего значения 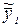 , которая может рассматриваться как ошибка измерения, подчиненная нормальному закону распределения с
, которая может рассматриваться как ошибка измерения, подчиненная нормальному закону распределения с 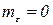 и
и 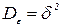 . Средняя ошибка измерений в точке х = xi, равная
. Средняя ошибка измерений в точке х = xi, равная 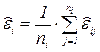 . также есть нормально распределенная случайная величина с параметрами
. также есть нормально распределенная случайная величина с параметрами 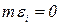 и
и 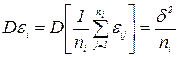
С учетом сказанного можно считать, что в каждой точке xi проводится одно наблюдение выходной переменной с результатом 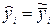 и случайной ошибкой
и случайной ошибкой 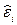
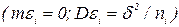 . То есть
. То есть 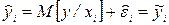 . Уравнение линейной регрессии будет иметь вид
. Уравнение линейной регрессии будет иметь вид 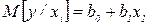 . Для того чтобы результаты расчетов параметров уравнения регрессии с использованием МНК и его анализа не менялись, необходимо полученное значение выходной переменной в точке xi брать с весом wi т.е.
. Для того чтобы результаты расчетов параметров уравнения регрессии с использованием МНК и его анализа не менялись, необходимо полученное значение выходной переменной в точке xi брать с весом wi т.е. 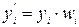 . В качестве веса wi будем брать величину, обратно пропорциональную дисперсии ошибки наблюдения в данной точке,
. В качестве веса wi будем брать величину, обратно пропорциональную дисперсии ошибки наблюдения в данной точке, 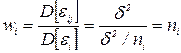 т. е. числу наблюдений.
т. е. числу наблюдений.
Тогда в соответствии с МНК задача поиска оценок b0 и b1 сводится к минимизации выражения, эквивалентного старому (3.2). в виде взвешенной сумме квадратов
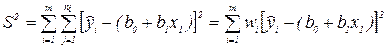
Это приводит к тем же расчетным соотношениям, что и ранее. Результаты анализа полученного уравнения регрессии также не меняются. Если число наблюдений во всех точках xi одинаково, то и все wi=n=const, i=l,...,m. Введение весовых коэффициентов wi позволяет проводить линейный регрессионный анализ для разноточных наблюдений.
 2014-02-13
2014-02-13 1582
1582
