Планы эксперимента для линейных моделей

Прежде чем перейти к построению плана эксперимента, необходи­мо определить область проведения эксперимента 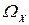Для этого снача­ла задают границы области определения факторов исходя из условий их физической допустимости. После этого определяется локальная по­добласть, в которой планируется проведение эксперимента. В качест­ве исходной точки (центр плана) обычно выбирают точку, которая соответствует наилучшим условиям функционирования системы, опреде­ленным на основании априорной информации о ее поведении. Если эта точка лежит на границе (или близко к ней) области изменения факто­ров, то центр плана сдвигают относительно нее для возможности варьирования переменных в обе стороны.

Величина интервалов варьирования переменных 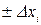выбирается таким образом, чтобы они были не меньше ошибки измерения самих факторов и не выводили значения факторов x_i за допустимую область их значений. При этом должна использоваться априорная информация о кривизне поверхности отклика, диапазоне изменения зависимой пере­менной у, ошибках измерения и т.п. (например, чем ниже точность фиксации факторов x_i, меньше кривизна поверхности отклика у(х) и уже диапазон изменения ее возможных значений, тем шире должен быть интервал варьирования факторов). Однако общих рекомендаций не су­ществует.

После выбора центральной точки Х⁰ и интервалов варьирования 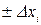переходят к построению собственного плана эксперимента.

Для построения линейных моделей наибольшее распространение получили двухуровневые планы, когда каждая из переменных x_i прини­мает значение на одном из двух уровней x₁^H и x₁^B, симметрично рас­положенных относительно центра плана (нулевого уровня): 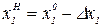; 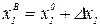. При переходе к стандартизированной за­писи переменных это соответствует +1 для x₁^B и -1 для x₁^H

(i=1,...,k).

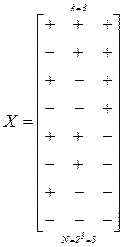
Множество всех возможных точек в k-мерном пространстве, коорди­наты которых x_i равны соответственно ±1, называется полным фактор­ным планом (ПФК) типа 2^k и соответствует вершинам k-мерного гипер­куба. Число точек полного факторного плана равно N=2^k. Для k = 1, 2, 3 матрица плана будет

, ,

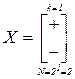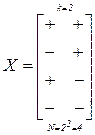Как видно. ПФП 2^k+1 может быть легко получен из ПФП 2^k расши­рением его по формуле вида

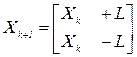
где L = [1,1,...,1] - вектор-столбец, состоящий из 2^К единиц.

Полный факторный план дает возможность получить независимые коэффициенты регрессии, соответствующие не только линейным эффектам (b_i, i=0,...,k), но и всем эффектам взаимодействия, т.е. коэффициенты b_ij...1 для эффектов x_i x_j... x₁, I,j,…,1=l,...,k, 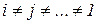в полиномиальной модели вида:

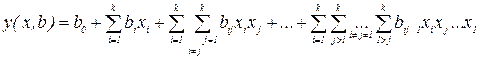
Общее число коэффициентов равно: K=l+k+C_k²+C_k³+...+С_k^k=2^k. Однако, если ограничиваться только линейными эффектами, то ПФП обладает большой избыточностью 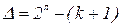(при к=5. 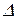=26; к=10, 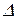=1013).