Интерпретация одного из алгоритмов решения задачи в терминах ДП

Задача минимизации

Динамическое программирование (ДП)

ДП - универсальный метод решения экстремальных задач (т.е. задач поиска минимума и мксимума функции).

Рассмотрим ДП как процесс построения множеств частичных решений исходной задачи и выбора из этих множеств доминирующих решений, причем таких, что хотя бы одно из них может быть "достроено" до оптимального.

f (x) —> min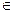, xX

Будем формировать множества X₀, X₁,..., X_n частичных решений,

где множество X_{k+ 1} получается из множества X_k путем " достраивания " каждого ρешения из X_k-1

Оптимальное решение x* выбирается из множества X_n.

Пусть

B = (k,b₁,..., b_i) – - состояние – - набор параметров (переменных состояния),связанный с каждым частичным решением x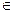X_k

X_k (B) – множество частичных решений x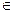X_k в состоянииB

B (x) – состояние частичного решения x

S – множество всех возможных состояний (пространство состояний) частичных решений

F(B) – функция доминирования, такая, что

частичное решение в состоянии B и максимизирующее (минимизирующее) F(B)

доминирует все остальные частичные решения в состоянии B т.е. это решение может быть достроено до полного допустимого решения с наименьшим значением целевой функции среди всех полных допустимых решений, достроенных из любого частичного решения в состоянииB.

=> в каждом множестве X_k(B) достаточно выбрать доминирующее решение для дальнейших построений.

В методе ДП рекуррентно вычисляют F(B) и находят состояние, соответствующее оптимальному решению.

Затем восстанавливают само оптимальное решение.

Для применения метода ДП необходимо корректно определить:

1. Пространство состояний S

2. Функцию доминирования F(B ), B 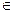S,

3. Способ построения частичных решений x' 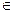X_k+l из частичных решений x 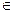X_k

4. Метод вычисления состояния B(x'), используя состояние B(x), если x' 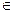X_k+1 достроен из x 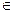X_k ·,

и рекуррентную формулу для вычисления значений F(B).

* * *

Пример алгоритма ДП. Формулировка задачи (минимизации суммарного штрафа за невыполнение директивных сроков): Служащий должен выполнить n работ к заданному сроку d. Для каждой работы j задана длительность выполнения p_j и штраф w_j, выплачиваемый в случае завершения работы j после d. Найти такую последовательность выполнения работ, чтобы суммарный штраф был наименьшим.

При заданной последовательности работ (i₁,…,i_n) момент завершения выполнения каждой работы i:

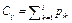
Введем переменные Uj: U_j = 1, если работа j является запаздывающей (Cj > d), и U_j = 0, если j является ранней (C_j < d).

Формулировка задачи ДП: Найти такую последовательность работ, чтобы минимизировать значение суммы штрафов

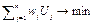
при условиях

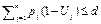
(т.е. суммарная длительность ранних работ д.б. не больше директивного срока) и U_j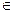{0,1}, j = 1,...,n.

Заметим, что на значение целевой функции влияет лишь информация о том, какие работы являются запаздывающими, а какие ранними. Поэтому существует оптимальная последовательность работ, в которой все ранние работы упорядочены произвольно и все запаздывающие работы упорядочены произвольно и расположены после последней ранней работы.

Пусть U* = (U*,..., Un) - оптимальный вектор для этой задачи и

W* - соответствующее значение целевой функции.

Будем формировать частичные решения, определяя переменные U_j = 0 и U_j = 1 для j = 1,…, n.

Будем говорить, что частичное решение (U₁,..., U_k) находится в состоянии (k, a), если определены значения переменных U₁,..., U_k и значение ограничения равно a т.е.

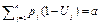
Пространство состояний. Переменные состояния могут принимать значения k= 0,1,…,n и a= 0,1,...,d.

Из начального состояния (0,0) можно перейти в (1,0), при котором U₁ = 1, либо в состояние (1,p₁), где U₁ = 0, если p₁<d.

В состояние (k, a) k {2, …, n} можно перейти только из состояния (k - 1, a), если U_k = 1, либо из состояния (k - 1,a - p_k), если U_k = 0.

Функция доминирования F(k, a) определяется как наименьшее значение целевой функции

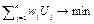
вычисленное для решений в состоянии (k, a)

Из определения целевой функции следует, что оптимальное значение целевой функции

W* = min{F (n,a)\a = 0,1,...,d}.

Значения F(k, a) могут быть вычислены рекуррентно. Для начала вычислений положим F(0, 0)=0 для (k, a)=(0,0) и F(k,a)=∞ для всех (k, a)≠(0,0).

F(k, a) = min{F(k — 1,a)+ w_k, F(k — 1,a — p_k)},

k = 1,...,n, a = 0,1,...,d.

При этом, если F(k, a) = F(k — 1, a) + w_k, то в частичном решении, соответствующем состоянию (k,a), перемениая U_k= 1 (запаздывающее решение). Если же F(к, a) = F(к — 1,a — p_k), то в этом решении U_k = 0 (раннее решение).