Основной вопрос теории систем линейных уравнений состоит в выяснении условий совместности системы. Ответ на этот вопрос дает
Теорема 5.1 (Кронекера-Капелли). Система линейных уравнений совместна тогда и только тогда, когда ранг основной матрицы системы равен рангу расширенной матрицы: Rg A = Rg A *.
Следствие. Линейная система имеет единственное решение при условии, что ранг основной и расширенной матриц равен числу ее неизвестных: Rg A = Rg A * = n.
Теорема Кронекера-Капелли утверждает существование решения, но она не дает никакого практического способа для нахождения всех решений системы. Однако при помощи теоремы Кронекера-Капелли можно исследовать систему, не находя ее решений. Если найден какой-либо базисный минор основной матрицы системы, то можно указать какие уравнения будут базисными, тогда остальные уравнения можно просто отбросить, т.к. они являются линейной комбинацией базисных уравнений; можно также указать какие неизвестные будут основными, а какие свободными, т.е. указать от скольких параметров зависит общее решение системы.
Пример 5.4. Исследовать систему линейных уравнений:
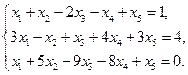
Решение. Найдем ранги основной и расширенной матриц системы:
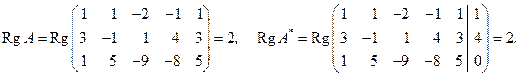
Поскольку ранги основной и расширенной матриц равны, то исходная система совместна. Выберем какой-либо базисный минор. Пусть это будет минор, составленный из элементов 1-й и 2-й строки и 1-го и 2-го столбца. Тогда первые два уравнения будут базисными, а третье уравнение можно отбросить. Неизвестные x 1 и x 2, в соответствии с выбранным базисным минором, будут основными, а все остальные – свободными, которые мы перенесем в правую часть. В результате получаем следующую эквивалентную систему линейных уравнений:
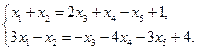
Решая эту систему уравнений, получим
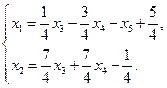
Эти равенства определяют общее решение системы, придавая свободным неизвестным произвольные числовые значения, можно получить все значения исходной системы. Это решение можно записать в более компактной форме. Пусть x 3=4 a, x 4=4 b, x 5= c. Тогда получим
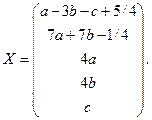 à
à
Пример 5.5. Исследовать на совместность и найти общее решение системы в зависимости от значений параметра l:
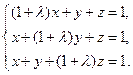
Решение. Выпишем основную матрицу системы и найдем ее определитель
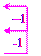

Если det A ¹0, т.е. если l¹0 и l¹–3, то ранги основной и расширенной матриц равны 3 (почему?). В этом случае система будет иметь единственное решение, которое можно найти, например, при помощи правила Крамера:
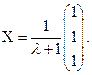
Если detA=0, то система будет либо несовместной, либо неопределенной.
Пусть l=0, тогда расширенная матрица системы будет иметь вид
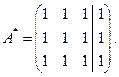
Видно, что ранги расширенной и основной матриц равны 1. В этом случае нужно оставить только одно уравнение
x + y + z = 1.
Тогда общее решение будет иметь вид
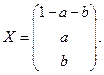
Пусть l=–3, тогда

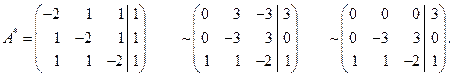
Видно, что ранг основной матрицы Rg A =2, а ранг расширенной матрицы Rg A *=3, следовательно, исходная система при l=–3 несовместна. à
 2014-02-13
2014-02-13 7569
7569








