Понятие матрицы. Виды матриц

Операции над матрицами и их свойства.

Понятие определителя второго и третьего порядков. Свойства определителей и их вычисление.

3. Общее описание задания.

4. Выполнение заданий.

5. Оформление отчета о лабораторной работе.

6. Анализ

Глоссарий

Выучите определения следующих терминов:

матрица, виды матриц, размерность матрицы, сумма матриц, свойства операции сложения матриц, умножение матрицы на число, произведение матриц, возведение матрицы в степень, транспонирование матрицы, обратная матрица, определитель матрицы, алгебраическое дополнение, минор элемента.

№ п/п	Новые понятия	Содержание
	Матрица размера	это прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, образующие матрицу, называются ее элементами.
	Матрица-строка	это матрица, состоящая из одной строки;
	Матрица-столбец	это матрица, состоящая из одного столбца.
	Квадратная матрица n -го порядка	это матрица, у которой количество строк равно количеству столбцов и равно n.
	Диагональная матрица	это квадратная матрица, у которой все элементы, кроме элементов, стоящих на главной диагонали равны нулю
	Единичная матрица	это диагональная матрица, у которой элементы, стоящие на главной диагонали равны единице.
	Умножение матрицы на число	Чтобы умножить матрицу на число k, необходимо на это число умножить все элементы матрицы
	Сложение матриц	Чтобы сложить две матрицы одинакового размера, необходимо сложить соответствующие элементы этих матриц
	Умножение матриц	а) Две матрицы можно перемножить тогда и только тогда, когда количество столбцов в первом сомножителе равно количеству строк во втором сомножителе. б) Произведением матрицы на матрицу является матрица , каждый элемент которой , стоящий на пересечении i -й строки и j -го столбца, равен сумме произведений элементов i -й строки матрицы A и j -го столбца матрицы B, т.е. .
	Транспонирование матрицы	Чтобы транспонировать матрицу A необходимо ее строки заменить столбцами с теми же номерами.
	Определитель квадратной матрицы второго порядка A =	равен разности произведений элементов главной диагонали и элементов побочной диагонали матрицы, т.е. D2= = .
	Определитель квадратной матрицы третьего порядка A =	D3= = .

№ п/п	Новые понятия	Содержание
	Алгебраическим дополнением элемента квадратной матрицы A n -го порядка	называется число, которое находят по формуле: ,
	Минором k-го порядка матрицы A размера m х n ()	называется определитель квадратной матрицы k -го порядка, состоящей из элементов, стоящих на пересечении произвольно выбранных k строк и k столбцов матрицы A. Обозначение: Mk - минор k -го порядка.
	Ранг матрицы	Рангом матрицы называют наивысший порядок отличных от нуля миноров этой матрицы. Обозначение: rangA или r (A).
	Обратная матрица для квадратной матрицы А	Обратной матрицей для квадратной матрицы A называется матрица A -1, такая, что верно равенство: A×A-1= A -1× A = E.
	Вырожденная и невырожденная матрицы	Квадратная матрица называется вырожденной, если ее определитель равен нулю, в противном случае матрица называется невырожденной.

ХОД ЗАНЯТИЯ

1. Инструктаж по ТБ в компьютерном классе.

2. На лабораторном занятии используется работа в парах (или малых группах).

Студентам необходимо:

- ознакомиться с основными теоретическими сведениями по каждой

из рассматриваемых тем;

- ответить на контрольные вопросы по по каждой

из рассматриваемых тем;

- изучить решение общих исходных практических заданий;

- выполнить представленные задания для малых групп;

- оформить отчет о лабораторной работе;

- защитить лабораторную работу

Основные теоретические сведения по теме:

"Матрицы. Основные операции с матрицами"

Матрица —это прямоугольный массив чисел, записанный в форе строк и столбцов: А= .

Каждое число в матрице называется элементом матрицы.

Размерностью матрицы называется совокупность двух чисел, состоящая из числа её строк m и числа столбцов n.

Если m=n, то матрицу называют квадратной матрицей порядка n.

Операции над матрицами: транспонирование матрицы, умножение (деление) матрицы на число, сложение и вычитание, умножение матрицы на матрицу.

Переход от матрицы А к матрице А^т, строками которой являются столбцы, а столбцами —строки матрицы А, называется транспонированием матрицы А.

Пример: А= , А^т = .

Чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на это число.

Пример: 2А= 2· = .

Суммой (разностью) матриц А и В одинаковой размерности называется матрица С=А В, элементы которой равны с_ij = a_ij b_ij для всех i и j.

Пример: А = ; В = . А+В= = .

Произведением матрицы А_{m n} на матрицу В_{n k} называется матрица С_{m k}, каждый элемент которой c_ij равен сумме произведений элементов i-ой строки матрицы А на соответствующий элемент j-го столбца матрицы В:

c_ij= a_i1· b_1j + a_i2·b_2j +…+ a_in·b_nj.

Чтобы можно было умножить матрицу на матрицу, они должны быть согласованными для умножения, а именно число столбцов в первой матрице должно быть равно числу строк во второй матрице.

Пример: А= 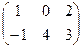и В = .

А·В—невозможно, т.к. они не согласованы.

В·А= . = = .

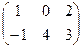Свойства операции умножения матриц.

1. Если матрица А имеет размерность m n, а матрица В—размерность n k, то произведение А·В существует.

Произведение В·А может существовать, только когда m=k.

2.Умножение матриц не коммутативно, т.е. А·В не всегда равно В·А даже если определены оба произведения. Однако если соотношение А·В= В·А выполняется, то матрицы А и В называются перестановочными.

3. Операция умножения матриц ассоциативна, т.е.

(А·В)·С = А·(В·С).

4. Операция умножения матриц дистрибутивна по отношению к алгебраическому сложению:

А·(В С) = А·В А·С;

(А В) С= А·С В·С.

5. Если произведение А·В определено, то для любого числа верно соотношение

(А·В) = ( А)·В = А·( В).

6. Если определено произведение А·В, то определенно произведение В^т·А^т и выполняется равенство

(А·В) ^т = В^т·А^т.

(А·В·С) ^т = С^т ·В^т·А^т,

при условии, что определено произведение матриц А·В·С.

7. Матрицу А можно умножить саму на себя только если она квадратная.

8. Произведение двух матриц может дать нулевую матрицу, хотя ни одна из матриц-сомножителей не является нулевой.

Две матрицы называются эквивалентными или равносильными (но не равными), если одна из них может быть получена из другой элементарными преобразованиями.

Элементарные преобразования матриц:

- перемена местами двух строк (столбцов);

- умножение строки (столбца) на число, отличное от нуля;

- прибавление (вычитание) к элементам одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число;

- отбрасывание строки (столбца), целиком состоящий из нулей.

Необходимый для повторения теоретический материал по теме:

"Определители второго, третьего и высших порядков.

Их свойства и методы вычисления"

Определителем (детерминантом) -го порядка квадратной матрицы называется сумма слагаемых, каждое из которых равно где - произведение элементов матрицы , взятых по одному из каждой строки и каждого столбца, а - число инверсий в перестановке, составленных из номеров столбцов.

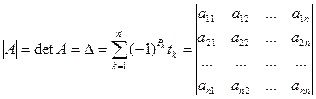
Определитель 2-го порядка находится по определению:

.

Пример. Вычислить .

Решение. .

Определитель 3-го порядка можно найти с помощью мнемонических правил.

Пример. Вычислить .

Решение.

1) .

2) .

Минором элемента называется определитель матрицы порядка, полученный вычёркиванием -ой строки -го столбца.

Алгебраическим дополнением элемента называется .

Теорема разложения Лапласа:

Детерминант квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.

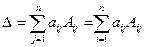
Пример. Вычислить .

Решение. .

Свойства определителей n-го порядка:

1) Величина определителя не изменится, если строки и столбца поменять местами.

2) Если определитель содержит строку (столбец) из одних нулей, то он равен нулю.

3) При перестановке двух строк (столбцов) определитель меняет знак.

4) Определитель, имеющий две одинаковые строки (столбца), равен нулю.

5) Общий множитель элементов любой строки (столбца) можно вынести за знак определителя.

6) Если каждый элемент некоторой строки (столбца) представляет собой сумму двух слагаемых, то определитель равен сумме двух определителей, в каждом из которых все строки (столбцы), кроме упомянутой, такие же, как и в данном определителе, а в упомянутой строке (столбце) первого определителя стоят первые слагаемые, второго – вторые.

7) Если в определителе две строки (столбца) пропорциональны, то он равен нулю.

8) Определитель не изменится, если к элементам некоторой строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.

9) Определители треугольных и диагональных матриц равны произведению элементов главной диагонали.

Метод накопления нулей вычисления определителей основан на свойствах определителей.

Пример. Вычислить .

Решение. Вычтем из первой строки удвоенную третью, далее используем теорему разложения по первому столбцу.

~ .

Контрольные вопросы (ОК-1, ОК-2, ОК-11,ПК-1):

1. Что называется определителем второго порядка?

2. Какие основные свойства определителей?

3. Что называется минором элемента?

4. Что называется алгебраическим дополнением элемента определителя?

5. Как разложить определитель третьего порядка по элементам какой-либо строки (столбца)?

6. Чему равна сумма произведений элементов какой-либо строки (или столбца), определителя по алгебраическим дополнениям соответствующих элементов другой строки (или столбца)?

7. В чём заключается правило треугольников?

8. Как вычисляются определители высших порядков способом понижения порядка

9. Что такое прямоугольная матрица?

10. Какая матрица называется квадратной? Нулевой? Что такое матрица-строка, матрица-столбец?

11. Какие матрицы называются равными?

12. Дать определения операций сложения, умножения матриц, умно­жения матрицы на число

13. Каким условиям должны удовлетворять размеры матриц при сло­жении, умножении?

14. В чём заключаются свойства алгебраических операций: коммута­тивность, ассоциативность, дистрибутивность? Какие из них выпол­няются для матриц при сложении, умножении, а какие нет?

15. Что такое обратная матрица? Для каких матриц она определена?

16. Сформулировать теорему о существовании и единственности обратной матрицы.

17. Сформулировать лемму о транспонировании произведения мат­риц.

Практические задания общие (ОК-1, ОК-2, ОК-11,ПК-1):

№1. Найти сумму и разность матриц А и В:

а)

б)

в)

№2. Выполните указанные действия:

а) С=2А+3В

б) D=А-3С

в) Z= -11А+7В-4С+D

если

№3. Выполните указанные действия:

а)

б)

в)

№4. При помощи применения четырех способов вычисления определителя квадратной матрица, найти определители следующих матриц:

а)

в)

№5. Найти определителей n-ого порядка, по элементам столбца (строки):

а) б)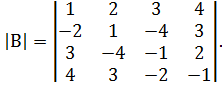

№6. Найти определитель матрицы, используя свойства определителей:

а) б)

Задания для работы в парах (ОК-1, ОК-20, ОК-22):

№1. Проверьте справедливость формулы (АВ)С=А(ВС), для матриц:

.

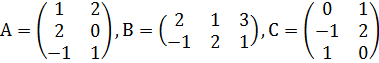№2. Проверьте справедливость формулы А(В+С)=АВ+АС, для матриц:

.

№3. Проверьте справедливость формулы , для матриц:

.

№4. Проверьте справедливость формулы , для матриц:

.

№5. Вычислить определитель матрицы любым из четырех предложенных способов:

.

.

№6. Найдите определители, используя известные вам способы:

а) б)

Тесты для работы в парах по теме «Матрицы и определители» (ОК-1, ОК-2, ОК-11,ПК-1):

1. Дана матрица . Отметьте верные высказывания об этой матрице:

это матрица размера ;

это квадратная матрица;

это матрица размера ;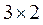

;

.

2. Дана матрица . Отметьте верные высказывания:

это квадратная матрица третьего порядка;

это единичная матрица;

элементы образуют главную диагональ матрицы;

это матрица размера ;

все элементы матрицы, находящиеся вне главной диагонали

равны нулю.

3. Пусть Е – единичная матрица порядка 4. Отметьте верные высказывания:

в матрице Е 16 элементов;

в матрице Е 12 нулевых элементов;

после транспонирования матрицы Е все ее нулевые элементы

заменяются единицами;

транспонирование не изменяет матрицу Е;

Е + Е = Е.

4. Пусть А – произвольная матрица 3-го порядка, Е – единичная матрица того же порядка. Отметьте верные равенства:

;

;

;

;

.

5. Отметьте верные утверждения:

операция сложения выполняется только над матрицами одинакового размера;

операция транспонирования сохраняет размер любой матрицы;

квадратные матрицы произвольных порядков согласованы;

чтобы умножить матрицу на скаляр, надо каждый элемент матрицы умножить на этот скаляр;

при умножении матрицы размера на матрицу размера получается матрица размера .

6. Укажите такие операции, которые нельзя выполнять над квадратными матрицами порядка 4:

вычитать;

складывать;

умножать друг на друга;

делить на число, отличное от нуля;

делить друг на друга.

7. Равенство выполняется

для всех единичных матриц произвольного порядка;

только для единичных матриц произвольного порядка;

для всех квадратных матриц;

только для квадратных матриц;

для произвольной матрицы А.

8. Равенство А + В = В + А выполняется

для произвольных матриц А, В одинакового размера;

для квадратных матриц одинакового порядка;

только для квадратных матриц одинакового порядка;

только, если одна из квадратных матриц А или В является единичной матрицей;

только, если обе матрицы являются единичными матрицами одинакового порядка.

9. Равенство справедливо

для любых согласованных матриц А и В;

если хотя бы одна из матриц является единичной матрицей,

согласованной с другой матрицей;

для произвольных квадратных матриц одинакового порядка;

если хотя бы одна из матриц является матрицей вида (где – произвольная константа), а другая – с ней согласована;

если одна из матриц является вектор - столбцом, а другая – согласованной с первой вектор – строкой.

10. Операция умножения матрицы А на себя выполнима

для произвольной матрицы А;

для квадратной матрицы А;

только для квадратной матрицы А;

для единичной матрицы А;

только для единичной матрицы А.