Лекция 5. ЛИНЕЙНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
Рассмотрим уравнение вида
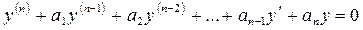 , (5.1)
, (5.1)
в котором коэффициенты 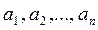 - постоянные вещественные числа, это уравнение будет называться линейным однородным уравнением, т.к. его правая часть равна нулю.
- постоянные вещественные числа, это уравнение будет называться линейным однородным уравнением, т.к. его правая часть равна нулю.
Функция 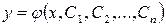 называется общим решением уравнения n -го порядка, если при соответствующем выборе произвольных постоянных С 1, С 2, С 3 ,…, Сn эта функция является решением любой задачи Коши, поставленной для данного уравнения. Всякое решение, получаемое из общего решения при конкретных значениях постоянных С 1, С 2, С 3 ,…, Сn, называется частным решением этого уравнения.
называется общим решением уравнения n -го порядка, если при соответствующем выборе произвольных постоянных С 1, С 2, С 3 ,…, Сn эта функция является решением любой задачи Коши, поставленной для данного уравнения. Всякое решение, получаемое из общего решения при конкретных значениях постоянных С 1, С 2, С 3 ,…, Сn, называется частным решением этого уравнения.
Для уравнения n -го порядка можно также как и для уравнений первого порядка можно поставить задачу Коши, которая состоит в том, чтобы найти решение уравнения, удовлетворяющее условиям:
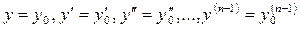 при
при 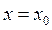 , (5.2)
, (5.2)
где 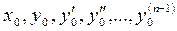 - заданные числа, которые называются начальными данными, или начальными условиями. Кроме того, однородное линейное (5.1) уравнение всегда имеет нулевое решение
- заданные числа, которые называются начальными данными, или начальными условиями. Кроме того, однородное линейное (5.1) уравнение всегда имеет нулевое решение 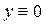 и оно удовлетворяет нулевым начальным условиям
и оно удовлетворяет нулевым начальным условиям
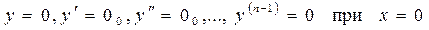 , (5.3)
, (5.3)
причем других решений с такими же начальными условиями, нет.
Для построения общего решения однородного линейного уравнения (5.1) достаточно знать п линейно независимых в интервале [a,b] частных решений 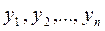 , т.е. таких решений, для которых тождество
, т.е. таких решений, для которых тождество
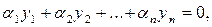 a < x < b,
a < x < b,
где 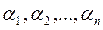 - постоянные числа, может выполняться только в том случае, когда
- постоянные числа, может выполняться только в том случае, когда 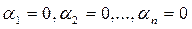 . Такая система решений называется фундаментальной. Для того, чтобы система решений
. Такая система решений называется фундаментальной. Для того, чтобы система решений 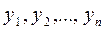 была фундаментальной необходимо и достаточно, чтобы решения
была фундаментальной необходимо и достаточно, чтобы решения 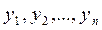 были линейно независимыми, а также ее определитель, который называется определителем Вронского или вронскианом
были линейно независимыми, а также ее определитель, который называется определителем Вронского или вронскианом
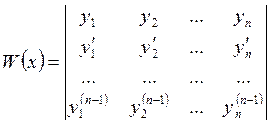 , (5.4)
, (5.4)
должен быть отличным от нуля 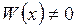 хотя бы в одной точке из интервала [a,b]. Для того, чтобы определить линейную независимость двух решений у 1 и у 2, необходимо вычислить отношение этих решений и, если они неравны константе, т.е.
хотя бы в одной точке из интервала [a,b]. Для того, чтобы определить линейную независимость двух решений у 1 и у 2, необходимо вычислить отношение этих решений и, если они неравны константе, т.е. 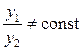 или
или 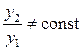 , то полученные решения будут линейно независимыми и из них можно составлять общее решение исходного уравнения.
, то полученные решения будут линейно независимыми и из них можно составлять общее решение исходного уравнения.
Пример 1. Дано уравнение: 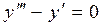 . Составляют ли фундаментальную систему решений функции
. Составляют ли фундаментальную систему решений функции 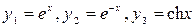 , являющиеся решениями этого уравнения?
, являющиеся решениями этого уравнения?
▲ Фундаментальная система решений должна состоять из линейно независимых решений исходного уравнения. Поэтому необходимо выяснить являются ли функции 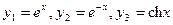 линейно независимыми. Для этого вычислим вронскиан (5.4):
линейно независимыми. Для этого вычислим вронскиан (5.4):
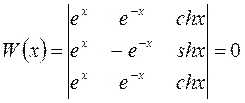 .
.
Этот определитель равен нулю, так как элементы 1-й и 3-й строк одинаковы. Следовательно, функции 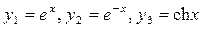 являются линейно зависимыми, а поэтому они не могут составлять фундаментальную систем. Таким образом, составить общее решение по этим частным решениям
являются линейно зависимыми, а поэтому они не могут составлять фундаментальную систем. Таким образом, составить общее решение по этим частным решениям 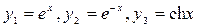 нельзя. ▲
нельзя. ▲
Фундаментальная система решений 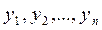 однородного уравнения (5.1) называется нормированной в точке х = х 0, если эти решения удовлетворяют соответственно следующим начальным условиям:
однородного уравнения (5.1) называется нормированной в точке х = х 0, если эти решения удовлетворяют соответственно следующим начальным условиям:
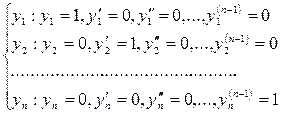 при х = х 0.
при х = х 0.
Если найдена фундаментальная система решений 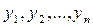 однородного уравнения (5.1), то формула
однородного уравнения (5.1), то формула
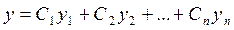 , (5.5)
, (5.5)
где 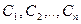 - произвольные постоянные, дает общее решение этого уравнения в области
- произвольные постоянные, дает общее решение этого уравнения в области
a < x < b, 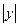 < +¥,
< +¥, 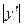 < +¥, …,
< +¥, …, 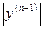 < +¥.
< +¥.
Все решения уравнения (5.1) содержаться в формуле (5.5).
Рассмотрим метод нахождения общего решения уравнения (5.1), который предложил Эйлер. Суть его заключается в том, что частное решение уравнения (5.1) ищется в виде
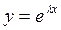 , (5.6)
, (5.6)
где l - некоторое вещественное или комплексное постоянное число, подлежащее определению.
Найдя производные решения (5.6)
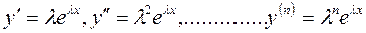 ,
,
и подставляя их, а также функцию (5.6) в уравнение (5.1), будем иметь
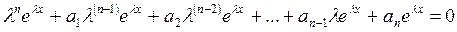 , (5.7)
, (5.7)
т.к. экспонента - 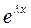 никогда неравна нулю, то поделив это уравнение на
никогда неравна нулю, то поделив это уравнение на 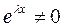 , получим алгебраическое уравнение вида
, получим алгебраическое уравнение вида
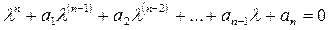 , (5.8)
, (5.8)
которое называется характеристическим уравнением, а его корни – характеристическими числами уравнения (5.8).
Структура фундаментальной системы решений 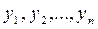 , а также общего решения уравнения (5.1) зависит от вида корней характеристического уравнения (5.8).
, а также общего решения уравнения (5.1) зависит от вида корней характеристического уравнения (5.8).
Рассмотрим правила построения фундаментальной системы, общего решения однородного уравнения.
Правило 1. Если все корни характеристического уравнения (5.8) действительные и различные числа, то есть 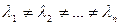 , то соответствующее им частные решения
, то соответствующее им частные решения
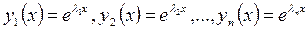
образуют фундаментальную систему, следовательно, общее решение уравнения (5.1) в этом случае имеет вид:
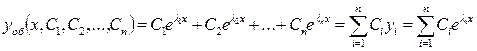 , (5.9)
, (5.9)
где 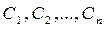 - произвольные постоянные.
- произвольные постоянные.
Правило 2. Среди корней характеристического уравнения (5.8) имеются комплексно-сопряженные, то есть 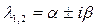 .
.
Соответствующее корню 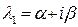 решение принимает мнимую форму:
решение принимает мнимую форму:
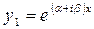 .
.
Чтобы освободиться от мнимой формы, преобразуем это решение по формуле Эйлера:
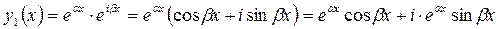 .
.
Отсюда выделяем действительные части, получаем два линейно независимых частных решения уже в вещественной форме:
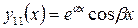 и
и 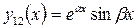 . (5.10)
. (5.10)
Теперь рассмотрим решение соответствующее корню 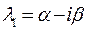 :
:
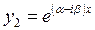 .
.
Освободимся от мнимой формы, преобразуем это решение по формуле Эйлера:
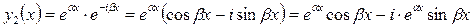 .
.
Отсюда выделяем действительные части, получаем два линейно независимых частных решения уже в вещественной форме:
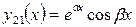 и
и 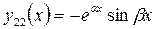 . (5.11)
. (5.11)
Анализируя полученные решения (5.10) и (5.11) приходи к выводу, что решения (5.10) являются линейно зависимыми с решениями (5.11), поскольку их отношения 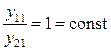 и
и 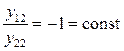 , и поэтому решения
, и поэтому решения 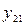 и
и 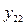 не могут входить в фундаментальную систему решений.
не могут входить в фундаментальную систему решений.
Таким образом, фундаментальная система решений будет состоять из частных решений (5.10), а компонента общего решения уравнения (5.1) соответствующая корням 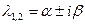 будет иметь вид
будет иметь вид
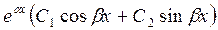 . (5.12)
. (5.12)
Если корни характеристического уравнения исключительно мнимые: 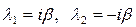 , то соответствующими независимыми частными решениями будут решения вида
, то соответствующими независимыми частными решениями будут решения вида
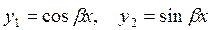 .
.
Следовательно, корням 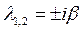 в формуле общего решения уравнения (5.1) соответствует выражение вида
в формуле общего решения уравнения (5.1) соответствует выражение вида
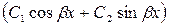 , (5.13)
, (5.13)
где 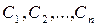 - произвольные постоянные.
- произвольные постоянные.
Правило 3. Среди корней характеристического уравнения имеются кратные.
3.1. Пусть среди корней характеристического уравнения есть действительные кратные корни 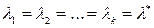 , то корню l * кратности k соответствуют k линейно независимых частных решения
, то корню l * кратности k соответствуют k линейно независимых частных решения
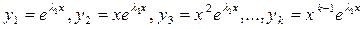 ,
,
а соответствующая компонента общего решения уравнения (5.1) имеет вид:
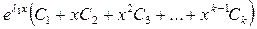 , (5.14)
, (5.14)
где 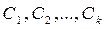 - произвольные постоянные.
- произвольные постоянные.
3.2. Пусть среди корней характеристического уравнения есть комплексный корень 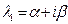 кратности k, а это значит, что есть также и сопряженный ему корень
кратности k, а это значит, что есть также и сопряженный ему корень 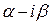 той же кратности. В этом случае паре
той же кратности. В этом случае паре 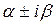 корней соответствуют 2 k линейно независимых частных решения:
корней соответствуют 2 k линейно независимых частных решения:
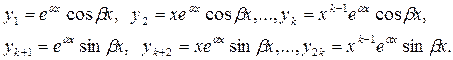
Следовательно, соответствующая компонента общего решения уравнения (5.1) имеет вид:
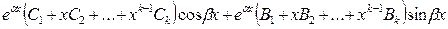 , (5.15)
, (5.15)
где 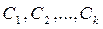 и
и 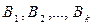 - произвольные постоянные.
- произвольные постоянные.
 2014-02-12
2014-02-12 702
702








