Модели законов распределения времени до отказа

По своей физической сущности отказы элементов и уст­ройств явля­ются событиями случайными. Поэтому для количест­венного описания отка­зов и вообще показателей надежности при­годны приемы теории вероятно­стей.

Анализируя отказы, нетрудно установить, что случайной величиной, описывающей отказы, является время до отказа (в общем случае наработка до отказа).

Установлено, что время до отказа, или, что то же самое, время безот­казной работы, неплохо описывается следующими моделями законов рас­пределения:

а)экспоненциальной;

б) моделью Вейбулла;

в) нормальной;

г) логарифмически нормальной.

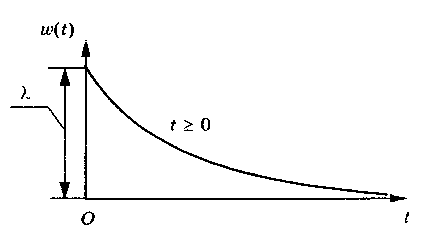
Для экспоненциальной модели плотность распределения времени до отказа описывается выражением (рис.1.2)

(1)

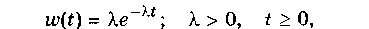
где λ— параметр модели (распределения).

Рис.1.2. Экспоненциальное распределение времени до отказа

В теории и практике
надежности РЭУ часто
употребляюттермин "экспоненциальный за­кон надежности", имея в виду, что время до отказа распределено по экспоненциаль­ной мо­дели.

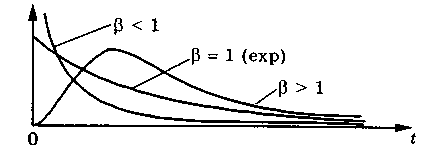
(2)

Для модели Вейбуллаплотность распреде­ле­ния времени до отказаописывается вы­ражением

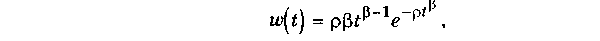
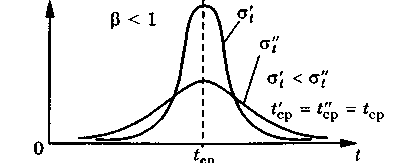
Рис.1.3 Распределение времени до отказа по за­кону Вейбулла

где ρ, в — параметры модели (распределения).

Параметр β называ­ют коэф­фициентом формы. От зна­чения того коэффициента во многом зависит график функции щt (рис.1.3).

При значении Р = 1 имеем дело с чисто экс­поненциальным распределе­нием, оно является частным случаем модели Вейбулла. При Р = 2...3 распределение Вейбулла в значительной степени при­ближается к нор­мальному распределению.

При нормальной модели плотность распределения времени до от­каза описывается выражением

(1.3)

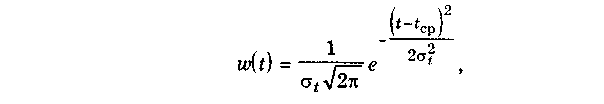
где t_ср, у_t — параметры модели (распределения).

Здесь t_ср — среднее время безотказной работы;

у_t — среднее квадратичное отклонение времени безотказ­ной работы.

Для нормальной модели вид функции щt показан на рис.1. 4.

щt

В случае нормальной модели говорят об усеченном распре­
делении, ибо область отрицательных значений времени до отказа
отбрасывают (отсекают), как не имеющую физического смысла.
Для логарифмически нормальной модели харак­терно то, что по нормаль­ному закону распределено не время до отказа, а лога­рифм этого времени.

Проводя испытания

Рис.1.4. Распределение времени до отказа по нормальному закону

элементов или устройств на на­дежность и фиксируя время до отказа каждого изделия, получим ряд значений случайной величины — времени до отказа. Общеприня­тыми прие­мами математической статистики для времени до отка­за можно построить гистограмму распределения (рис.1.5) и попы­таться восстановить вид функции щ(t)

Величины щ_i* определяют по формуле

(1.4)

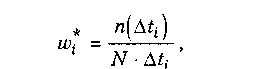
где N — общее число испытываемых изделий;

n(Дt_i) — число изделий, отказавших на интервале времени Дt_iДt_i — ширина 1-го временного интервала.

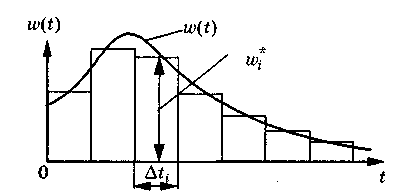С увеличением ко­личества испытываемых изделий N и уменьшением ширины интерва­лов Дt_i гистограмма все более и более приближается к плотно­сти распределения щt

Рис.1.5. Гистограмма распределения времени до отказа

Характеристика щt на прак­тике не находит ши­рокого при­менения в качестве показателя надежности изделий, однако без знания этой характеристики трудно опреде­лить интересующие нас показатели надежности.