Полумарковские модели

Если при описании Марковского процесса предположить что с момента перехода изделия в состояние 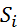до перехода в 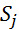случайное время нахождение изделия в состоянии 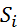подчиняется произвольному распределению , то такой процесс называется полумарковским или неоднородным Марковским процессом, а моделирование этого процесса полумарковской моделью. Полумарковские модели позволяют значительно полнее описать процессы изменения состояний в реальных системах с периодическим контролем. Формальное описание полумарковского процесса сводиться к следующему: имеется конечное множество состояний Sпереходы из состояния 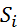в состояние 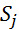совершаются в случайные моменты времени. Все состояния связаны в Марковскую цепьи характеризуются вероятностями перехода 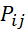образующих матрицу P. Переход в 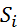осуществляется в момент времени , а следующее в , то промежуток обозначается и задаётся семейством функций распределений значений интервалов времени пребывания в i-ом состоянии, т.о. каждой паре индексов i, j соответствует распределение , которое . Т.о. в отличии от Марковского процесса полумарковский задаётся двумя матрицами –вероятность перехода из

Имеется возможность задать полу матрицы одной матрицей

-представляют собой вероятность того что из исходного состояния S_i изделие переходит в состояние S_j и время пребывания изделия в состоянии S_i не превзойдет величины t.