Говорят, что случайная величина 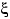 имеет биномиальное распределение с параметрами
имеет биномиальное распределение с параметрами 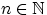 и
и 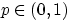 , и пишут:
, и пишут: 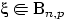 , если
, если 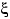 принимает значения
принимает значения 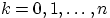 с вероятностями
с вероятностями 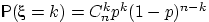 . Случайная величина с таким распределением имеет смысл числа успехов в
. Случайная величина с таким распределением имеет смысл числа успехов в 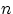 испытаниях схемы Бернулли с вероятностью успеха
испытаниях схемы Бернулли с вероятностью успеха 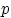 . Таблица распределения
. Таблица распределения 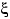 имеет вид:
имеет вид:

Распределение Бернулли совпадает с распределением 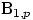 .
.
Дискретная случайная величина Х имеет биномиальное распределение с параметрами n€N и p€(0,1), если принимает значение k=0,1,….n с вероятностями
P(X=k)= Ckn pkqn-k q=1-p
15 Распределение Пуассона, параметры распределения.
Дискпетная случайная величина Х имеет распределение Пуассона с параметром ħ>0, если Х принимает значения к=0,1,2…n с вероятностями, определенными формулой пуассона
P(X=k)= 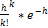
При рассмотрении маловероятных событий, имеющих место в большой серии независимых испытаний некоторое (конечное) число раз, вероятности появления этих событий подчиняются закону Пуассона или закону редких событий 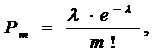 , где λ равна среднему числу появления событий в одинаковых независимых испытаниях, т.е. λ = n × p, где p – вероятность события при одном испытании, e = 2,71828, m -частота данного события, математическое ожидание m равно l.
, где λ равна среднему числу появления событий в одинаковых независимых испытаниях, т.е. λ = n × p, где p – вероятность события при одном испытании, e = 2,71828, m -частота данного события, математическое ожидание m равно l.
Закон Пуассона можно применять для совокупностей, достаточно больших по объему (n > 100) и имеющих достаточно малую долю единиц, обладающих данным признаком (p < 0,1).
При этом распределение Пуассона можно применить, когда на только не известно значение n – общего числа возможных результатов, но и когда не известно конечное число, которое n может представлять. Там, где есть среднее число случаев наступления события, вероятность наступления события описывается членами разложения:
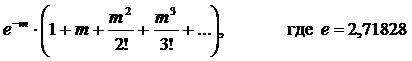 .
.
Поэтому соответствующие вероятности равны:
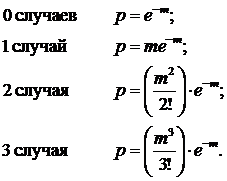
16 Функция распределения вероятностей одномерной случайной величины. Свойства функции распределения.


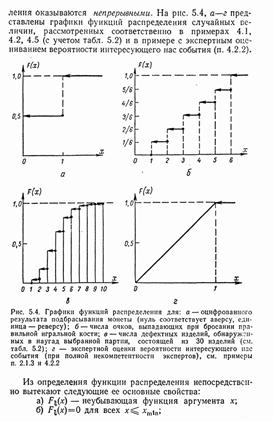

№17.Статистические гипотезы. Ошибки I рода и II рода. Уровень значимости. Общая схема проверки статистической гипотезы
Пусть в (статистическом) эксперименте доступна наблюдению случайная величина X, распределение которой  известно полностью или частично. Тогда любое утверждение, касающееся
известно полностью или частично. Тогда любое утверждение, касающееся 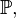 называется статистической гипотезой. Гипотезы различают по виду предположений, содержащихся в них:
называется статистической гипотезой. Гипотезы различают по виду предположений, содержащихся в них:
- Статистическая гипотеза, однозначно определяющая распределение  , то есть
, то есть 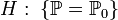 , где
, где 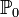 какой-то конкретный закон, называется простой.
какой-то конкретный закон, называется простой.
-Статистическая гипотеза, утверждающая принадлежность распределения  к некоторому семейству распределений, то есть вида
к некоторому семейству распределений, то есть вида 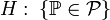 , где
, где  -семейство распределений, называется сложной.
-семейство распределений, называется сложной.
Ошибки первого рода и ошибки второго рода в математической статистике — это ключевые понятия задач проверки статистических гипотез. Тем не менее, данные понятия часто используются и в других областях, когда речь идёт о принятии «бинарного» решения (да/нет) на основе некоего критерия (теста, проверки, измерения), который с некоторой вероятностью может давать ложный результат.
Ошибку первого рода часто называют ложной тревогой, ложным срабатыванием или ложноположительным срабатыванием — например, анализ крови показал наличие заболевания, хотя на самом деле человек здоров. Ошибку второго рода иногда называют пропуском события или ложноотрицательным срабатыванием — человек болен, но анализ крови этого не показал
Вероятность ошибки первого рода при проверке статистических гипотез называют уровнем значимости и обычно обозначают греческой буквой 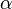 . Вероятность ошибки второго рода не имеет какого-то особого общепринятого названия, на письме обозначается греческой буквой
. Вероятность ошибки второго рода не имеет какого-то особого общепринятого названия, на письме обозначается греческой буквой 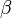
Обе эти характеристики обычно вычисляются с помощью так называемой функции мощности критерия. В частности, вероятность ошибки первого рода есть функция мощности, вычисленная при нулевой гипотезе. Для критериев, основанных на выборке фиксированного объема, вероятность ошибки второго рода есть единица минус функция мощности, вычисленная в предположении, что распределение наблюдений соответствует альтернативной гипотезе. Для последовательных критериев это также верно, если критерий останавливается с вероятностью единица (при данном распределении из альтернативы).
Этапы проверки стат.гипотез:
1) Формулировка основной гипотезы 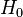 и конкурирующей гипотезы
и конкурирующей гипотезы 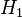
2) Задание уровня значимости 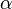 , на котором в дальнейшем и будет сделан вывод о справедливости гипотезы. Он равен вероятности допустить ошибку первого рода.
, на котором в дальнейшем и будет сделан вывод о справедливости гипотезы. Он равен вероятности допустить ошибку первого рода.
3) Расчёт статистики 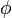 критерия такой, что:
критерия такой, что:
- её величина зависит от исходной выборки
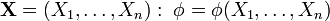
- по её значению можно делать выводы об истинности гипотезы 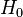
- сама статистика 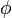 должна подчиняться какому-то известному закону распределения, так как сама
должна подчиняться какому-то известному закону распределения, так как сама 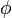 является случайной в силу случайности
является случайной в силу случайности 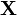
4) Построение критической области. Из области значений 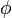 выделяется подмножество
выделяется подмножество 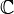 таких значений, по которым можно судить о существенных расхождениях с предположением. Его размер выбирается таким образом, чтобы выполнялось равенство
таких значений, по которым можно судить о существенных расхождениях с предположением. Его размер выбирается таким образом, чтобы выполнялось равенство
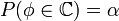 .Это множество
.Это множество 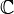 и называется критической областью.
и называется критической областью.
4) Вывод об истинности гипотезы. Наблюдаемые значения выборки подставляются в статистику 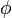 и по попаданию (или непопаданию) в критическую область
и по попаданию (или непопаданию) в критическую область 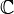 выносится решение об отвержении (или принятии) выдвинутой гипотезы
выносится решение об отвержении (или принятии) выдвинутой гипотезы 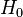
№18.Проверка гипотезы о числовом значении математического ожидания нормального распределения при неизвестной диспресии.Односторонняя и двусторонняя критическая область.
В этом случае за основу проверки гипотезы 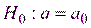 , где
, где 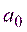 - – заранее заданное число, положен критерий
- – заранее заданное число, положен критерий 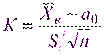 , где
, где 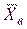 ,
,  - – случайные величины, вычисляемые по формулам и. Этот критерий при выполнении гипотезы (5.19) имеет
- – случайные величины, вычисляемые по формулам и. Этот критерий при выполнении гипотезы (5.19) имеет 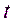 - распределение с числом степеней свободы k=n-1, т.е.
- распределение с числом степеней свободы k=n-1, т.е.
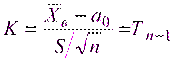 , где
, где 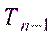 - – случайная величина, подчиняющаяся распределению Стьюдента
- – случайная величина, подчиняющаяся распределению Стьюдента
№19.Проверка гипотезы о равенстве дисперсий двух нормальных распределений.
Пусть Х и Y – две случайные величины, имеющие нормальные распределения и неизвестные дисперсии 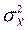 и
и 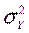 . Требуется проверить гипотезу
. Требуется проверить гипотезу 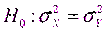
Построим критерий для проверки этой гипотезы. Для этого рассмотрим исправленные дисперсии:
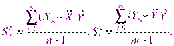
Как известно,эти величины могут быть приняты за приближенные значения 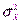 и
и 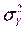
Имеют место следующие распределения 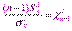 Поэтому в соответствии с определением F-распределения (см. п. 4.1) отношение
Поэтому в соответствии с определением F-распределения (см. п. 4.1) отношение 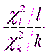 или отношение
или отношение 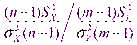 будет иметь распределение Фишера с
будет иметь распределение Фишера с 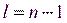 и
и 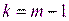 степенями свободы, т.е.
степенями свободы, т.е. 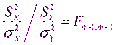 Если гипотеза верна, то непосредственно получаем критерий
Если гипотеза верна, то непосредственно получаем критерий 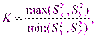 который подчиняется распределению Фишера с l и k степенями свободы
который подчиняется распределению Фишера с l и k степенями свободы
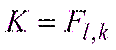
№20.Выборочная оценка коэффициента корреляции.Проверка гипотезы о значимости коэффициента корреляции.
№21.Основные понятия теории вероятности и матем статистики
Одним из основных понятий теории вероятностей является понятие события. Под событием понимают любой факт, который может произойти в результате опыта или испытания. Под опытом, или испытанием, понимается осуществление определённого комплекса условий.
Примеры событий:
– попадание в цель при выстреле из орудия (опыт — произведение выстрела; событие — попадание в цель);
– выпадение двух гербов при трёхкратном бросании монеты (опыт — трёхкратное бросание монеты; событие — выпадение двух гербов);
– появление ошибки измерения в заданных пределах при измерении дальности до цели (опыт — измерение дальности; событие — ошибка измерения).
Можно привести бесчисленное множество подобных примеров. События обозначаются заглавными буквами латинского алфавита A,B,C и т.д.
Различают события совместные и несовместные. События называются совместными, если наступление одного из них не исключает наступления другого. В противном случае события называются несовместными. Например, подбрасываются две игральные кости. Событие A — выпадание трех очков на первой игральной кости, событие B — выпадание трех очков на второй кости. A и B — совместные события. Пусть в магазин поступила партия обуви одного фасона и размера, но разного цвета. Событие A — наудачу взятая коробка окажется с обувью черного цвета, событие B — коробка окажется с обувью коричневого цвета, A и B — несовместные события.
Событие называется достоверным, если оно обязательно произойдет в условиях данного опыта.
Событие называется невозможным, если оно не может произойти в условиях данного опыта. Например, событие, заключающееся в том, что из партии стандартных деталей будет взята стандартная деталь, является достоверным, а нестандартная — невозможным.
Событие называется возможным, или случайным, если в результате опыта оно может появиться, но может и не появиться. Примером случайного события может служить выявление дефектов изделия при контроле партии готовой продукции, несоответствие размера обрабатываемого изделия заданному, отказ одного из звеньев автоматизированной системы управления.
События называются равновозможными, если по условиям испытания ни одно из этих событий не является объективно более возможным, чем другие. Например, пусть магазину поставляют электролампочки (причем в равных количествах) несколько заводов-изготовителей. События, состоящие в покупке лампочки любого из этих заводов, равновозможны.
Важным понятием является полная группа событий. Несколько событий в данном опыте образуют полную группу, если в результате опыта обязательно появится хотя бы одно из них. Например, в урне находится десять шаров, из них шесть шаров красных, четыре белых, причем пять шаров имеют номера.А - появление красного шара при одном извлечении, B- появление белого шара, C — появление шара с номером. События A,B,C образуют полную группу совместных событий.
Введем понятие противоположного, или дополнительного, события. Под противоположным событием 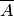 понимается событие, которое обязательно должно произойти, если не наступило некоторое событие A. Противоположные события несовместны и единственно возможны. Они образуют полную группу событий. Например, если партия изготовленных изделий состоит из годных и бракованных, то при извлечении одного изделия оно может оказаться либо годным — событие A, либо бракованным — событие
понимается событие, которое обязательно должно произойти, если не наступило некоторое событие A. Противоположные события несовместны и единственно возможны. Они образуют полную группу событий. Например, если партия изготовленных изделий состоит из годных и бракованных, то при извлечении одного изделия оно может оказаться либо годным — событие A, либо бракованным — событие 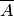
Математическая (или теоретическая) статистика опирается на методы и понятия теории вероятностей, но решает в каком-то смысле обратные задачи.
В теории вероятностей рассматриваются случайные величины с заданным распределением или случайные эксперименты, свойства которых целиком известны. Предмет теории вероятностей — свойства и взаимосвязи этих величин (распределений).
Но часто эксперимент представляет собой черный ящик, выдающий лишь некие результаты, по которым требуется сделать вывод о свойствах самого эксперимента. Наблюдатель имеет набор числовых (или их можно сделать числовыми) результатов, полученных повторением одного и того же случайного эксперимента в одинаковых условиях.
При этом возникают, например, следующие вопросы: Если мы наблюдаем одну случайную величину — как по набору ее значений в нескольких опытах сделать как можно более точный вывод о ее распределении?
Если мы наблюдаем одновременно проявление двух (или более) признаков, т.е. имеем набор значений нескольких случайных величин — что можно сказать об их зависимости? Есть она или нет? А если есть, то какова эта зависимость?
Часто бывает возможно высказать некие предположения о распределении, спрятанном в «черном ящике», или о его свойствах. В этом случае по опытным данным требуется подтвердить или опровергнуть эти предположения («гипотезы»). При этом надо помнить, что ответ «да» или «нет» может быть дан лишь с определенной степенью достоверности, и чем дольше мы можем продолжать эксперимент, тем точнее могут быть выводы. Наиболее благоприятной для исследования оказывается ситуация, когда можно уверенно утверждать о некоторых свойствах наблюдаемого эксперимента — например, о наличии функциональной зависимости между наблюдаемыми величинами, о нормальности распределения, о его симметричности, о наличии у распределения плотности или о его дискретном характере, и т.д.
Итак, о (математической) статистике имеет смысл вспоминать, если
имеется случайный эксперимент, свойства которого частично или полностью неизвестны,
мы умеем воспроизводить этот эксперимент в одних и тех же условиях некоторое (а лучше — какое угодно) число раз.
Примером такой серии экспериментов может служить социологический опрос, набор экономических показателей или, наконец, последовательность гербов и решек при тысячекратном подбрасывании монеты.
 2015-01-21
2015-01-21 2454
2454