Для изучения динамики явления за ряд периодов возможно вычисление системы цепных и базисных индексов. Построение такой системы возможно в двух вариантах:
1. Оценивают относительное изменение уровня изучаемого явления по сравнению с каким-то одним определенным периодом времени. В этом случае строится система индексов с постоянной базой сравнения, то есть базисные индексы.
2. Оценивают относительное изменение уровня изучаемого явления по сравнению с предшествующим периодом. В этом случае строится система индексов с переменной базой сравнения, то есть цепные индексы.
Рассмотрим системы цепных и базисных индексов цен, физического объема продукции и стоимости продукции.
| Индексы | Базисные индексы | Цепные индексы |
| Индивидуальные индексы физического объема | 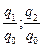 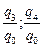 | 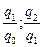 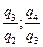 |
| Агрегатные индексы физического объема | 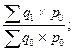 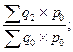 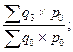 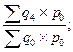 | 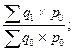 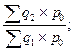 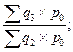 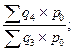 |
| Индивидуальные индексы цен | 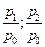 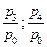 | 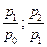 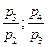 |
| Агрегатные индексы цен | 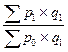 ; ; 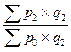 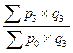 ; ; 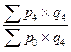 | 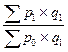 ; ; 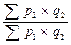 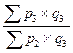 ; ; 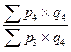 |
| Индивидуальные индексы стоимости | 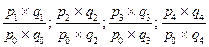 | 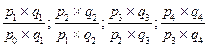 |
| Агрегатные индексы стоимости | 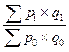 ; ;  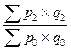 ; ; 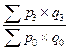 ; ; 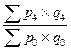 | 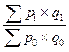 ; ;  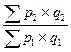 ; ; 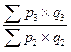 ; ; 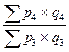 |
При исчислении индексов физического объема может быть применена другая система весов. Например, при исчислении отдельных индексов используются цены периода, предшествующего отчетному. Тогда получают следующий ряд цепных индексов:
J1/0= 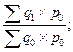 J2/1=
J2/1= 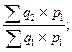 J3/2=
J3/2= 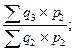 J4/3=
J4/3= 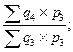
Для индивидуальных индексов цен, физического объема и стоимости справедливо следующее правило:
1. Произведение промежуточных по периодам цепных индексов дает базисный индекс последнего периода i4/0=i1/0  i2/1
i2/1  i3/2
i3/2  i3/4
i3/4
2. Отношение базисного индекса отчетного периода к базисному индексу предшествующего периода дает цепной индекс отчетного периода i3/4=i4/0:i3/0
Это правило позволяет применять так называемый цепной метод, то есть находить неизвестный ряд базисных индексов по известным цепным и обратно.
Имея два базисных агрегатных индекса физического объема с постоянным соизмерителем, можно получить цепной индекс отчетного периода.
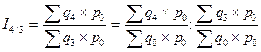
Базисный индекс отчетного периода может быть получен перемножением соответствующих цепных индексов, если соизмеритель принимается на уровне одного и того же периода:
I4/0= I1/0  I 2/1
I 2/1  I3/2
I3/2  I4/3
I4/3
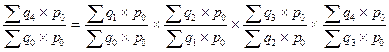
При использовании переменных соизмерителей цепной метод применять нельзя, так как цепные индексы в этом случае несопоставимы друг с другом.
Агрегатные индексы качественных показателей всегда являются индексами с переменными весами, так как соизмеритель всегда принимается на уровне отчетного периода. Поэтому цепной метод расчета индексов не применим к агрегатным индексам качественных показателей.
Сформулированное выше правило взаимосвязи цепных и базисных индексов в полном объеме применимо к агрегатным индексам стоимости.
Рассмотрим на примере расчет базисных и цепных индексов и проверим их взаимосвязь.
| Вид про- дукции | Произведено продукции, т (q) | Сопоста- вимая цена за 1 т, млн. руб. | ||||
| 1992 г. | 1993 г. | 1994 г. | 1995 г. | 1996 г. | (р0) | |
| 1. | ||||||
| 2. |
Во-первых, рассчитаем базисные (в % к 1992 г.) и цепные индексы физического объема каждого вида и всей продукции.
Базисные индексы:
| Индексы | По продукции № 1 | По продукции № 2 | По двум видам продукции в целом |
| 1993 г. к 1992 г. | 1050: 1000 = 1,05 | 550: 500 = 1,1 | (1050  100+550 100+550  200):(1000 200):(1000  100+ 500 100+ 500  200) = 1,08 200) = 1,08 |
| 1994 г. к 1992 г. | 1102: 1000 = 1,1 | 600: 500 = 1,2 | (1102  100+600 100+600  200): 200000 = 1,15 200): 200000 = 1,15 |
| 1995 г. к 1992 г. | 1158: 1000 = 1,16 | 650: 500 = 1,3 | (1158  100+650 100+650  200): 200000 = 1,23 200): 200000 = 1,23 |
| 1996 г. к 1992 г. | 1219: 1000 = 1,21 | 700: 500 = 1,4 | (1219  100+700 100+700  200):200000= 1,31 200):200000= 1,31 |
Цепные индексы:
| Индексы | По продукции № 1 | По продукции № 2 | По двум видам продукции в целом |
| 1993 г. к 1992 г. | 1050: 1000 = 1,050 | 550: 500 = 1,1 | (1050  100+550 100+550  200):(1000 200):(1000  100+ 500 100+ 500  200)=1,08 200)=1,08 |
| 1994 г. к 1993 г. | 1102: 1050 = 1,049 | 600: 550 = 1.091 | (1102  100+600 100+600  200):(1050 200):(1050  100+ 550 100+ 550  200)=1,071 200)=1,071 |
| 1995 г. к 1994 г. | 1158: 1102 = 1,051 | 650: 600 = 1,083 | (1158  100+650 100+650  200):(1102 200):(1102  100+ 600 100+ 600  200)=1,068 200)=1,068 |
| 1996 г. к 1995 г. | 1219: 1158 = 1,053 | 700: 650 = 1,077 | (2119  100+700 100+700  200):(1158 200):(1158  100+ 650 100+ 650  200)= 1,066 200)= 1,066 |
Во-вторых, проверим взаимосвязь исчисленных базисных и цепных индексов физического объема продукции:
а) произведение промежуточных по периодам цепных индексов дает базисный индекс последнего периода
I 96/92 = I93/92  I94/93
I94/93  I 95/94
I 95/94  I96/95
I96/95
1,31 = 1,08  1,071
1,071  1,068
1,068  1,066
1,066
б) отношение базисного индекса отчетного периода к базисному индексу предшествующего периода дает цепной индекс отчетного периода
I 96/95 = I 96/95: I 95/92
1,066 = 1,31: 1,23
 2015-01-21
2015-01-21 897
897







