Качественный показатель характеризует уровень изучаемого результативного показателя в расчете на количественную единицу и определяется как отношение данного результативного показателя к связанному с ним количественному показателю (фактору) на единицу которого он рассчитывается. Например, себестоимость единицы продукции “z” определяется как отношение суммы затрат на производство данного вида продукции “zq” к количеству продукции “q”.
Принципы построения индексов качественных показателей рассмотрим на примере расчета индексов себестоимости.
Индивидуальный индекс себестоимости характеризует изменение уровня себестоимости единицы какого-либо вида продукции в отчетном периоде по сравнению с базисным и вычисляется по формуле:
i z = z 1: z0.
Процент снижения или увеличения себестоимости рассчитывается как iz  100% - 100%.
100% - 100%.
С помощью индивидуального индекса себестоимости можно определить сумму экономии (перерасхода) от снижения себестоимости продукции данного вида. Для каждого отдельного вида продукции сумма экономии (перерасхода) вычисляется по формуле:
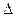 z = (z 1- z0)
z = (z 1- z0)  q,
q,
где z 1 и z 0 - себестоимость единицы продукции данного вида, в отчетном и базисном периоде, q1 - объём продукции данного вида в отчетном периоде.
Агрегатный индекс себестоимости показывает изменение общего уровня себестоимости разных видов продукции. Суммирование уровней себестоимости отдельных видов продукции не имеет экономического смысла, так как в этом случае не учитывается количество продукции, имеющей тот или иной уровень себестоимости. Поэтому для расчета индекса уровни качественного показателя необходимо взвесить на соответствующее значение связанного с ним количественного показателя (фактора). Обычно таким фактором выступает объём продукции.
При построении индексов качественных показателей следует руководствоваться следующим правилом: весами служат те или иные количественные показатели (чаще всего объём продукции), зафиксированные как правило на уровне отчетного периода.
Формулу общего агрегатного индекса себестоимости можно записать так:
Iz = 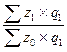 .
.
Числитель индекса показывает затраты на производство продукции отчетного периода, а знаменатель - величину затрат на производство продукции отчетного периода при уровне себестоимости базисного периода.
Взвешивание уровня себестоимости по количеству продукции отчетного периода позволяет увязать индексы количественных и качественных показателей в систему:
Izq = Iz  Iq или
Iq или 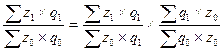
Используя величины индекса себестоимости можно рассчитать сумму экономии (перерасхода) от снижения себестоимости, которая рассчитывается как разность между числителем и знаменателем агрегатного индекса себестоимости:
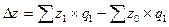 .
.
Если полученная разность имеет знак минус, то это означает экономию в затратах от снижения себестоимости, а знак плюс - потери от повышения себестоимости.
Рассмотрим на примере расчет индивидуальных и агрегатного индексов себестоимости и сумм экономии (перерасхода) от снижения себестоимости.
| Виды продукции | Фактически произведено продукции в отчетном периоде, млн. штук (q 1) | Cебестоимость еденицы продукции, тыс. руб. | |
| Базисный год (z0) | Oтчетный год (z1) | ||
| № 1 | 79,3 | 75,1 | |
| № 2 | 64,0 | 60,2 | |
| № 3 | 120,0 | 110,5 |
1. Определим изменение (в %) себестоимости в отчетном периоде по сравнению с базисным каждого изделия и всей продукции в целом. Для того, чтобы вычислить изменение себестоимости по каждому виду продукции следует рассчитать индивидуальные индексы, а по всей продукции в целом - агрегатный индекс.
а) индивидуальные индексы: i z = z1: z0
i z = 75,1: 79,3 = 0,947 или 94,7 %
i z = 60,2: 64,0 = 0,941 или 94,1 %
i z = 110,5: 120,0 = 0,921 или 92,1 %
б) агрегатный индекс себестоимости продукции
Iz = 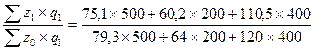 = 0,9334 или 93,34 %
= 0,9334 или 93,34 %
В отчетном периоде по сравнению с базисным себестоимость единицы продукции № 1 снизилась на 5,3 %, продукции № 2 - на 5,9 %, продукции № 3 - на 7,9 %, в целом по всей продукции - на 6,66 %.
2. Вычислим абсолютную величину экономии (перерасхода) от изменения себестоимости в отчетном периоде по сравнению с базисным по каждому виду продукции и по всей продукции в целом.
а) для каждого вида продукции: 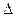 z =
z = 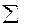 z 1
z 1  q1 - z0
q1 - z0  q1
q1
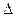 z = (75,1 - 79,3)
z = (75,1 - 79,3)  500 = - 2100 тыс.рублей
500 = - 2100 тыс.рублей
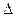 z = (60,2 - 64,0)
z = (60,2 - 64,0)  200 = - 760 тыс. рублей
200 = - 760 тыс. рублей
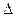 z = (110,5 - 120,0)
z = (110,5 - 120,0)  400 = - 3800 тыс. рублей
400 = - 3800 тыс. рублей
б) для всей продукции в целом: 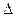 z =
z = 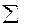 z 1 q1 -
z 1 q1 - 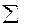 z0 q1
z0 q1
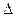 z = 93790 - 100450 = - 6600 тыс. рублей
z = 93790 - 100450 = - 6600 тыс. рублей
Экономия затрат от снижения себестоимости продукции составила 6600 тыс. рублей, в том числе по продукции № 1 - 2100 тыс. рублей, по продукции № 2 - 760 тыс. рублей, по продукции № 3 - 3800 тыс. рублей.
С помощью индексов можно охарактеризовать выполнение планового задания по росту или снижению того или иного показателя. Рассмотрим на примере расчет планируемого снижения себестоимости продукции (работ, услуг), выполнения плана по снижению себестоимости и размер снижения себестоимости по сравнению с предыдущим периодом.
| Вид продукции | Производство продукции, млн.штук | Себестоимость единицы про-дукции, тыс.рублей | ||||||
| в базисном году (q0) | по плану (qпл) | в отчетном году (q1) | в базисном году (z0) | по плану (zпл) | в отчетном году (z1) | |||
| 88,5 | 88,2 | |||||||
| 125,4 | 123,6 | |||||||
| 143,1 | 141,9 | |||||||
Для того, чтобы определить планируемое снижение себестоимости каждого вида продукции, следует соотнести себестоимость единицы продукции, предусмотренную планом, и себестоимость единицы продукции базисного года, то есть рассчитать индивидуальный индекс по формуле: i z = zпл.: z0.
Так, для продукции № 1 - i z = 88,5: 90 = 0,9833, то есть запланированный процент снижения себестоимости единицы продукции составляет 1,67 %. Для продукции № 2 - i z = 125,4: 126 = 0,9952 и запланированный процент снижения 0,48 %, для продукции № 3 - iz = 143,1: 144 = 0,9938 и запланированный процент снижения - 0,62 %.
Индекс, показывающий планируемое изменение затрат на производство всех видов продукции в отчетном периоде по сравнению с затратами на производство той же продукции в базисном периоде, определяется по формуле:
I z = 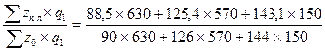 = 0,9905
= 0,9905
Величина данного агрегатного индекса показывает, что в целом по предприятию запланировано снижение себестоимости продукции в отчетном году на 0,95 %.
За счет снижения себестоимости продукции предприятие планирует экономию в размере:
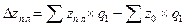 = 148698 - 150120 = - 1422 тыс. рублей
= 148698 - 150120 = - 1422 тыс. рублей
Для того, чтобы проконтролировать выполнение плана по снижению себестоимости продукции следует вычислить индексы динамики себестоимости продукции и сопоставить их с запланированными процентами снижения себестоимости продукции.
Индивидуальные индексы динамики себестоимости продукции рассчитываются по следующей формуле: i z = z1: z0. Для продукции № 1 индекс динамики себестоимости равен 0,98, для продукции № 2 - 0,981, для продукции № 3 - 0,9854. Таким образом, себестоимость в отчетном периоде по сравнению с базисным по продукции № 1 снизилась на 2 % при планируемом уровне снижения себестоимости на 1,67 %, по продукции № 2 - на 1,9 % при планируемом уровне снижения на 0,48 %, по продукции № 3 - на 1,46 % при планируемом уровне снижения на 0,62 %.
Индекс динамики себестоимости продукции предприятия можно вычислить по следующей формуле:
Iz = 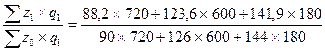 = 0,9813
= 0,9813
Снижение себестоимости продукции предприятия по сравнению с базисным годом составило 1,87 %. Фактическая экономия от снижения себестоимости продукции составила:
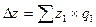 -
- 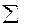 z0
z0  q1= 163206 - 166320 = - 3114 тыс. рублей.
q1= 163206 - 166320 = - 3114 тыс. рублей.
Для того, чтобы установить процент перевыполнения плана по снижению себестоимости продукции следует рассчитать индексы выполнения плана. Индивидуальные индексы выполнения плана вычисляются по следующей формуле: i z= z1: zпл.. Для продукции № 1 индекс выполнения плана равен 0,9966, для продукции № 2 - 0,9856, для продукции № 3 - 0,9916, то есть план по снижению себестоимости продукции № 1 перевыполнен на 0,34 %, по продукции № 2 - на 1,44 %, по продукции № 3 - на 0,84 %.
Процент выполнения плана по снижению себестоимости продукции предприятия определяют по следующей формуле:
Iz = 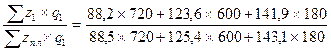 = 0,9908
= 0,9908
План по снижению себестоимости продукции перевыполнен предприятием на 0,92 %. Сумма сверхплановой экономии от снижения себестоимости продукции составила:
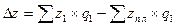 = 163206 - 164718 = -1512 тыс. рублей.
= 163206 - 164718 = -1512 тыс. рублей.
Сумма плановой и сверхплановой экономии (1422 тыс. рублей + 1512 тыс. рублей) от снижения себестоимости продукции не равна сумме фактической экономии (3114 тыс. рублей) в связи с изменением фактического объема производства отдельных видов продукции по сравнению c запланированным.
Средняя себестоимость единицы однородной продукции по группе предприятий определяется по формуле средней арифметической взвешенной: 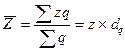 .
.
В качестве веса используется количество продукции данного вида, выпущенное отдельными предприятиями (q) или удельный вес каждого предприятия в общем объеме выпуска данного вида продукции (d q). Зная среднюю себестоимость единицы продукции в отчетном и базисном периодах, можно определить ее изменение в форме отношения двух взвешенных средних:
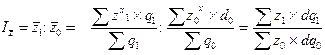 .
.
При исчислении средней себестоимости единицы продукции отчетного периода весами служит количество продукции отчетного периода, а при определении средней себестоимости единицы продукции базисного периода - количество продукции базисного периода. Отношение двух взвешенных средних с переменными весами, характеризующее изменение индексируемой величины, называется индексом переменного состава. Величина индекса переменного состава зависит от двух факторов: изменения уровня себестоимости на отдельных предприятиях и изменения в соотношении между объемами продукции, выпускаемой отдельными предприятиями.
Для того, чтобы измерить влияние изменений в структуре весов на показатель изменения уровня себестоимости продукции следует рассчитать отношение средних взвешенных с одними и теми же весами, то есть исчислить индекс постоянного состава.
Формула индекса средней себестоимости продукции постоянного состава выглядит следующим образом:
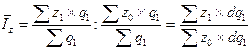 .
.
Средняя себестоимость продукции в базисном периоде скорректирована на структуру фактического выпуска продукции. Следовательно, данное отношение показывает каково было бы изменение среднего уровня себестоимости продукции по группе предприятий, если бы удельный вес предприятий с разным уровнем себестоимости в базисном периоде был таким же, как и в отчетном.
Как уже отмечалось выше, величина взвешенной средней зависит от двух факторов: изменения отдельных уровней индексируемой величины (значение “ z” на отдельных предприятиях) и от изменения в структуре весов. Поэтому, если веса не остаются постоянными, то индекс фиксированного состава будет отличаться от индекса переменного состава в меру отношения:
Id= 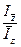 =
= 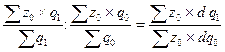 .
.
Указанное отношение принято называть индексом влияния структурных сдвигов, который представляет собой отношение среднего уровня себестоимости продукции базисного периода, скорректированного на отчетную структуру производства определенного вида продукции, и фактической средней себестоимости продукции базисного периода.
Рассмотрим на примере расчет индексов себестоимости продукции переменного, постоянного состава и структурных сдвигов.
| Номер предприятия | Выработано продукции в отчетном году, млн.штук | Себестоимость еди-ницы продукции в отчетном году, млн.руб. | Затраты на произ-водство продукции в базисном году, млн.руб | |||
| Базисный год (q0) | Отчетный год (q1) | Базисный год (z0) | Отчетный год (z1) | Базисный год (z 0q0) | Отчетный год (z 1q1) | |
| 1,18 | 1,16 | |||||
| 1,32 | 1,30 | |||||
| Итого | 1,20 | 1,18 |
Для оценки снижения уровня себестоимости единицы продукции по двум предприятиям в целом рассчитаем средние уровни себестоимости единицы продукции:
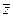 = 11024: 9200 = 1,20 млн. рублей
= 11024: 9200 = 1,20 млн. рублей
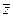 = 13212: 11240 = 1,18 млн. рублей
= 13212: 11240 = 1,18 млн. рублей
Далее, вычислим индекс себестоимости продукции переменного состава: 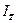 =
= 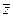 1:
1: 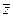 0 = 1,18: 1,20 = 0,983
0 = 1,18: 1,20 = 0,983
Средняя себестоимость единицы продукции по двум предприятиям в отчетном году по сравнению с базисным годом снизилась на 1,7 %.
Изменение средней себестоимости единицы продукции за счет изменения уровня себестоимости продукции на каждом предприятии оценивается индексом себестоимости продукции постоянного состава:
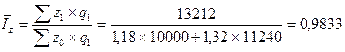
В среднем уровень себестоимости продукции снизился на каждом предприятии в отчетном периоде по сравнению с базисным на 1,67 %.
C помощью индекса влияния структурных сдвигов можно определить снижение средней себестоимости единицы продукции за счет перемещения объемов производства продукции на предприятие с более низкой себестоимостью:
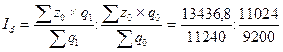 = 0,9975
= 0,9975
За счет изменения в соотношении выпуска продукции между предприятиями средняя себестоимость продукции снизилась в отчетном периоде по сравнению с базисным на 0,25 %.
Взаимосвязь индексов переменного, постоянного состава и структурных сдвигов можно описать следующим равенством:
Iz = Iz  Id 0,98 = 0,9833
Id 0,98 = 0,9833  0,9975
0,9975
В отдельных случаях могут быть известны не абсолютные значения индексируемых показателей, а их относительные изменения. В такой ситуации агрегатный индекс можно рассчитать косвенным путем, используя взвешенную среднюю из индивидуальных индексов, если нам известен размер результативной величины за отчетный период. Рассмотрим на примере расчет среднего гармонического индекса себестоимости продукции.
| Вид продукции | Издержки млн.руб. | прозводства, | Изменение себестоимости продукции, % |
| базисный год (z0q0) | отчетный год (z1q1) | (iz-100%) | |
| 174,6 | + 3 | ||
| - 5 |
Общий индекс себестоимости продукции можно рассчитать по следующей формуле: Iz= 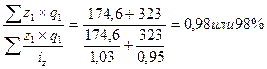
Исходя из того, что издержки производства представляют собой произведение количества выпущенной продукции (q) и себестоимости единицы продукции (z), мы можем построить следующую систему индексов:
Izq = Iq  Iz
Iz
где Izq - индекс издержек производства, Iq - индекс физического объема продукции и Iz - индекс себестоимости единицы продукции.
На основе такой системы индексов мы можем рассчитать общее изменение издержек производства в отчетном периоде по сравнению с базисным, а также изменение издержек производства за счет отдельных факторов в абсолютном и относительном выражении по приведенной ниже схеме.
1. Определим общее изменение издержек производства:
- относительное изменение вычислим с помощью индекса издержек производства
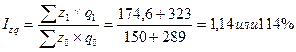 I
I
- абсолютное изменение рассчитаем как разность между числителем и знаменателем индекса издержек производства
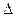 zq =
zq = 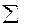 z 1
z 1  q1 -
q1 - 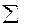 z0
z0  q0 = 58,6 млн. рублей.
q0 = 58,6 млн. рублей.
2. Определим изменение издержек производства за счет отдельных факторов:
а) за счет изменения себестоимости единицы продукции
- относительное изменение вычислим с помощью индекса себестоимости продукции Iz = 0,98 или 98 %
- абсолютное изменение рассчитаем как разность между числителем и знаменателем индекса себестоимости продукции
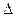 zqz =
zqz = 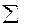 z 1
z 1  q1 -
q1 - 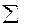 z0
z0  q1 = 497,6-509,5=-11,9 млн. рублей.
q1 = 497,6-509,5=-11,9 млн. рублей.
б) за счет изменения количества выпущенной продукции
- относительное изменение вычислим с помощью индекса физического объема продукции
Iq = Izq: Iz = 1,14: 0,98 = 1,16 или 116 %
- абсолютное изменение рассчитаем исходя из взаимосвязи исчисленных показателей
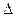 zq q =
zq q = 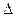 zq -
zq - 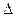 zqz = 58,6 + 11,9 = 70,5 млн. рублей
zqz = 58,6 + 11,9 = 70,5 млн. рублей
Таким образом, издержки производства в отчетном периоде по сравнению с базисным возросли на 14 % или 58,6 млн. рублей в результате увеличения производства продукции на 16 % или 70,5 млн. рублей при общем снижении себестоимости единицы продукции на 2 % или 11,9 млн. рублей.
В рыночной экономике особое место среди индексов качественных показателей отводится индексам цен. С помощью индекса цен можно оценить динамику цен на товары (работы, услуги) и измерить уровень инфляции.
Автором первой формулы агрегатного индекса цен является немецкий статистик Г. Пааше:
Ip = 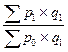 .
.
Немецкий ученый Э. Ласпейрес предложил определять индекс цен следующим образом:
Ip = 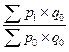 .
.
Индексируемой величиной обоих индексов являются цены. Весами в индексе цен Пааше выступает количество продукции текущего периода, а в индексе цен Ласпейреса - количество продукции базисного периода. Значение индексов цен Пааше и Ласпейреса не совпадают, так как индексы имеют различное экономическое содержание. Индекс цен Пааше показывает насколько товары (работы, услуги) в отчетном периоде стали дороже (дешевле), чем в базисном. Индекс цен Ласпейреса дает ответ на вопрос во сколько бы раз товары (работы, услуги) базисного периода подорожали (подешевели) из-за изменения цен на них в отчетном периоде. Согласно практике индекс цен, рассчитанный по формуле Пааше, имеет тенденцию некоторого занижения, а по формуле Ласпейреса - завышения темпов инфляции.
Индекс цен американского экономиста И. Фишера представляет собой среднюю геометрическую из произведений двух агрегатных индексов цен Ласпейреса и Пааше:
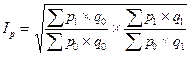 .
.
Геометрическая форма индексов имеет большой недостаток - она лишена конкретного экономического содержания. Так, в отличие от агрегатных индексов разность между числителем и знаменателем не покажет никакой реальной экономии (или потерь) из-за изменения цен или физического объема продукции. Индекс Фишера целесообразно использовать для исчисления индексов цен за длительный период времени для сглаживания тенденций в структуре и составе объема продукции.
Для пересчета стоимостных показателей из текущих цен в сопоставимые используется индекс-дефлятор, который является агрегированной формой индекса цен. Дефлятор - это коэффициент, переводящий значение стоимостного показателя за отчетный период в стоимостные измерители базисного. Индекс-дефлятор рассчитывается как отношение фактической стоимости продукции отчетного периода к стоимости объема продукции, структура которого аналогична структуре отчетного периода, но определенного в ценах базисного года. В основе расчета индекса-дефлятора лежит формула Пааше - агрегатная формула индекса цен с текущими весами. Важной особенностью индекса-дефлятора является то, что он не может быть использован для сравнительной оценки динамики цен за два периода. Индексы-дефляторы дают представление только об отношении стоимости продукции в текущем периоде к ее стоимости в базисном периоде без учета отличия состава и структуры продукции.
 2015-01-21
2015-01-21 4472
4472
