При интегрировании функций наиболее часто используются следующие его свойства:
1) 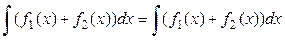 ;
;
2) 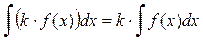 ;
;
3) 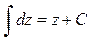 .
.
Пример 1. Найти 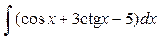 .
.
Решение. Воспользуемся свойствами 1-3, а также таблицей интегралов:
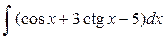 =
= 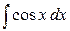 +3
+3 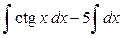 =
= 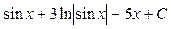 .
.
Ответ: 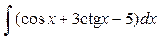 =
= 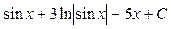 .
.
Одним из основных методов интегрирования является метод замены переменной (метод подстановки), который в некоторых случаях позволяет свести заданный интеграл к табличному интегралу.
Замена переменной под знаком неопределенного интеграла осуществляется по формулам:
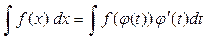
или
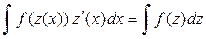 . (2)
. (2)
Пример 2. Найти 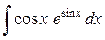 .
.
Решение. Воспользуемся формулой (2) и таблицей интегралов:
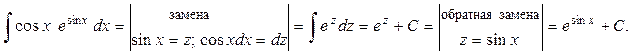 Ответ:
Ответ: 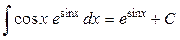 .
.
Этот интеграл можно взять, используя подведение под знак дифференциала части подинтегральной функции (не прописывая замену переменной)
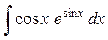 =
= 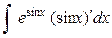 =
= 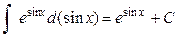 .
.
Наиболее часто прием подведения под знак дифференциала используется при линейной замене переменной интегрирования:
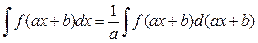 , (3)
, (3)
так как 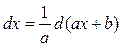 .
.
Пример 3. Найти 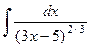 .
.
Решение. Согласно формуле (3) можно записать:
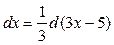
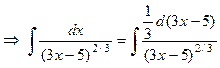 .
.
Теперь воспользуемся свойством 2, а также таблицей интегралов:
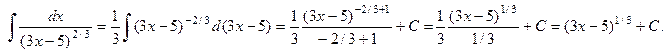 Ответ:
Ответ: 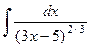 =
= 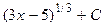 .
.
 2015-01-21
2015-01-21 500
500








