Производной функции 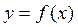 в точке х называется конечный предел отношения приращения функции
в точке х называется конечный предел отношения приращения функции 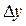 к приращению аргумента
к приращению аргумента 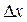 :
:
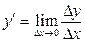 , (16)
, (16)
где 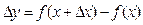 .
.
Другие обозначения производной: 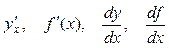 .
.
Если существует производная функции 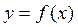 в точке х, то функция называется дифференцируемой в этой точке. Дифференцирование функции – это процесс нахождения производной
в точке х, то функция называется дифференцируемой в этой точке. Дифференцирование функции – это процесс нахождения производной 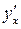 . При дифференцировании используют таблицу производных и правила дифференцирования.
. При дифференцировании используют таблицу производных и правила дифференцирования.
Таблица производных основных элементарных функций.
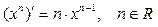 | |||
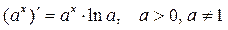 | 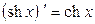 | ||
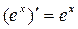 | 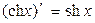 | ||
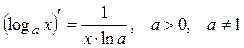 | 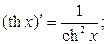 | ||
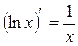 | 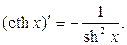 | ||
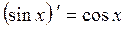 | 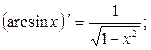 | ||
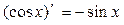 | 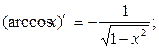 | ||
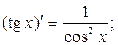 | 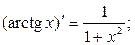 | ||
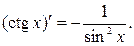 | 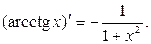 |
Основные правила дифференцирования.
1) Производная от постоянной равна нулю:
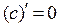 . (17)
. (17)
2) Производная алгебраической суммы (u 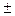 v) двух дифференцируемых функций
v) двух дифференцируемых функций 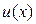 и
и 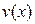 существует и равна алгебраической сумме производных этих функций:
существует и равна алгебраической сумме производных этих функций:
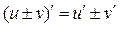 (18)
(18)
3) Производная произведения двух дифференцируемых функций 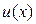 и
и 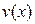 существует и вычисляется по формуле:
существует и вычисляется по формуле:
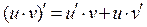 . (19)
. (19)
4) Производная отношения двух дифференцируемых функций 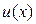 и
и 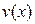 существует и вычисляется по формуле:
существует и вычисляется по формуле:
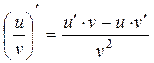 . (20)
. (20)
5) Постоянный множитель можно выносить за знак производной:
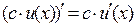 (21)
(21)
6) Производная от сложной функции: если 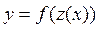 , где f (z) и z (x) –дифференцируемые функции, то
, где f (z) и z (x) –дифференцируемые функции, то 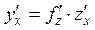 («правило цепочки»).
(«правило цепочки»).
7) Производная от функции,заданной неявно: если функция 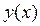 задана уравнением
задана уравнением 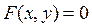 , то для нахождения
, то для нахождения 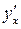 нужно продифференцировать обе части тождества
нужно продифференцировать обе части тождества 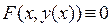 по аргументу х и из полученного равенства найти
по аргументу х и из полученного равенства найти 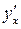 как решение линейного уравнения.
как решение линейного уравнения.
8) Производная от функций 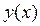 , заданной параметрически: если
, заданной параметрически: если 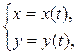 где x (t), y (t) – дифференцируемые функции, то:
где x (t), y (t) – дифференцируемые функции, то:
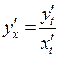 . (22)
. (22)
Производные высших порядков:производная 2-го порядка: 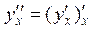 ,
,
3-го порядка: 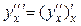 и т.д. Для обозначений производных высшего порядка используются также символы вида:
и т.д. Для обозначений производных высшего порядка используются также символы вида: 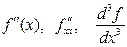 . Производные 4 и более высоких порядков обозначаются при помощи римских цифр:
. Производные 4 и более высоких порядков обозначаются при помощи римских цифр: 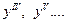 . Производная n -го порядка обозначается
. Производная n -го порядка обозначается 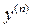 , она получается n -кратным дифференцированием функции
, она получается n -кратным дифференцированием функции 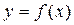 :
: 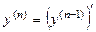 .
.
 2015-01-21
2015-01-21 10700
10700
