Характеристической функцией называется функция состояния ТС, позволяющая при соответствующем выборе независимых переменных (при определенных условиях сопряжения ТС с окружающей средой) выражать через свои производные наиболее просто и в явном виде термодинамические параметры, характеризующие свойства термодинамической системы. Построение термодинамического анализа на этих свойствах характеристических функций составляет основу метода характеристических функций.
Рассмотрим простую (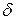 ℒ =0), закрытую (
ℒ =0), закрытую (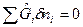 ) термодинамическую систему. Тогда для обратимых процессов объединенные выражения 1-го и 2-го законов термодинамики будут иметь вид:
) термодинамическую систему. Тогда для обратимых процессов объединенные выражения 1-го и 2-го законов термодинамики будут иметь вид:
 , (5)
, (5)
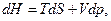 (6)
(6)
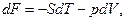 (7)
(7)
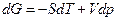 . (8)
. (8)
Каждое из уравнений (5)-(8) связывает пять переменных величин, которые зависят лишь от состояния ТС и не зависят от пути процесса. Функции U, H, F, G являются характеристическими только при определенном выборе независимых переменных: 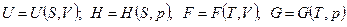 . Полные дифференциалы функций U, H, F, G имеют вид:
. Полные дифференциалы функций U, H, F, G имеют вид:
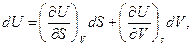 (9)
(9)
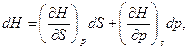 (10)
(10)
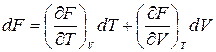 , (11)
, (11)
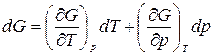 . (12)
. (12)
Линейным дифференциальным соотношениям (9)-(12) тождественны объединенные выражения 1-го и 2-го законов термодинамики (5)-(8). Сопоставляя уравнения (5) и (9) можно наиболее просто выразить неизвестные параметры – температуру Т и давление р с помощью частных производных внутренней энергии по энтропии S и по объему V:
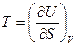 ,
, 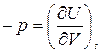 . (13)
. (13)
По аналогии выразим неизвестные параметры в выражениях (6)-(8) с помощью частных производных (10)-(12) для функций H, F и G:
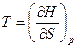 ,
, 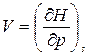 , (14)
, (14)
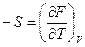 ,
, 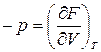 , (15)
, (15)
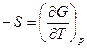 ,
, 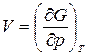 . (16)
. (16)
Согласно свойству полного дифференциала вторая смешанная производная от функции U не зависит от порядка дифференцирования, т.е.:
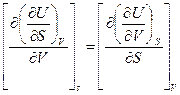 , или (17)
, или (17)
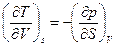 .
.
По аналогии для функций H, F, G получим:
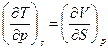 , для Н, (18)
, для Н, (18)
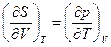 , для F, (19)
, для F, (19)
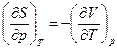 , для G. (20)
, для G. (20)
Уравнения (17)-(20) называются дифференциальными соотношениями взаимности или уравнениями Максвелла. Они в такой же степени достоверны, как и законы термодинамики, следствием которых они являются. Уравнения (17)-(20) широко используются при термодинамическом анализе. При анализе также широко используется уравнение связи, которое выводится следующим образом. Если функция 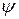 - функция состояния, то ее полный дифференциал равен:
- функция состояния, то ее полный дифференциал равен:
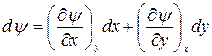 .
.
Для 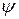 = const
= const 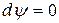 . Тогда получим:
. Тогда получим:
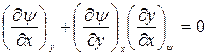 .
.
После деления на 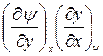 имеем:
имеем:
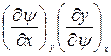
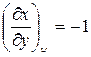 . (21)
. (21)
Связи частных производных одного термодинамического параметра по другому (21) справедливы при определенных условиях сопряжения ТС с окружающей средой.
Схема чередования термодинамических параметров в уравнении связи (21) имеет вид:
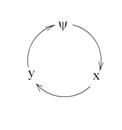
т.е. функция → аргумент → фиксированный параметр: (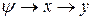 ), (
), (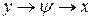 ), (
), (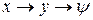 ).
).
 2015-01-21
2015-01-21 561
561








