Функция состояния ТС – энтропия может быть представлена в виде функциональной связи S=S (T,V). Дифференциал энтропии – полный дифференциал, т.е.
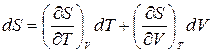 . (1)
. (1)
Разделим уравнение (1) на dT и умножим на Т при р= const. Тогда имеем:
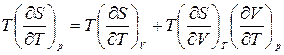 . (2)
. (2)
По определению 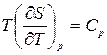 и
и 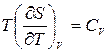 . После их подстановки в (2) получим:
. После их подстановки в (2) получим:
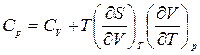 . (3)
. (3)
Производная 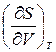 включает калорическую величину – энтропию и неудобна при расчетах. Поэтому заменим эту производную, используя соотношения взаимности Максвелла для смешанных производных от свободной энергии Гельмгольца:
включает калорическую величину – энтропию и неудобна при расчетах. Поэтому заменим эту производную, используя соотношения взаимности Максвелла для смешанных производных от свободной энергии Гельмгольца:
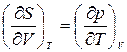 .
.
Тогда, используя уравнение связи в виде:
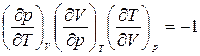 , получим:
, получим:
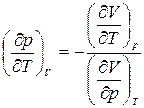 . (4)
. (4)
Подставим выражение (4) вместо 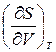 в (3) и получим:
в (3) и получим:
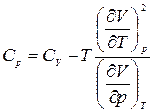 . (5)
. (5)
Покажем, как из уравнения (5) можно получить уравнение Майера для идеального газа, дифференцируя уравнение состояния:
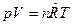 . Тогда
. Тогда 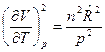 и
и 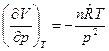 .
.
После подстановки этих производных в (5) получим:
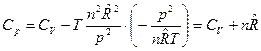 , Дж/К.
, Дж/К.
Таким образом, получили уравнение Майера для общих теплоемкостей Ср и СV системы:
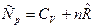 .
.
Получим связь между Ср и CV в другом виде, используя производные от натуральных логарифмов параметров и учитывая, что 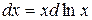 .
.
Тогда получим, что
|
|
|
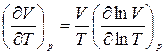 и
и 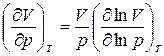 . (6)
. (6)
После подстановки выражений (6) в уравнение (5) с учетом, что 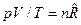 , окончательно получим связь между изобарной и изохорной теплоемкостями в общем виде:
, окончательно получим связь между изобарной и изохорной теплоемкостями в общем виде:
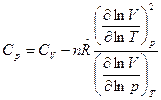 .
.
 2015-01-21
2015-01-21 2517
2517








