Энтропия равновесного процесса S- это функция состояния и ее дифференциал dS- полный дифференциал
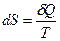 , [
, [ 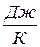 ] и
] и 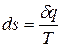 , [
, [ 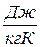 ].
].
Температура Т на границе ТС, где подводится теплота, есть интегрирующий делитель, превращающий неполный дифференциал – теплоту в полный дифференциал – энтропию. Для равновесного кругового процесса ∮ 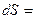 ∮
∮ 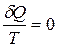 - интеграл Клаузиуса.
- интеграл Клаузиуса.
У всякой ТС существует однозначная функция состояния – энтропия, которая при адиабатных равновесных процессах не изменяется.
Для сложной открытой ТС, которая взаимодействует с окружающей средой, изменение энтропии dS связано с подводом теплоты 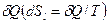 , с протеканием процессов внутри ТС
, с протеканием процессов внутри ТС 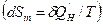 и с подводом массы вещества
и с подводом массы вещества 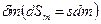 :
:
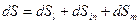 , Дж/К.
, Дж/К.
Для процессов, протекающих внутри ТС, 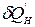 - «некомпенсируемая теплота» (Клаузиус), в которую превращается количество работы вследствие необратимости (неравновесности) процессов внутри системы.
- «некомпенсируемая теплота» (Клаузиус), в которую превращается количество работы вследствие необратимости (неравновесности) процессов внутри системы.
Если границу ТС пересекают несколько веществ с массами mi, то изменение энтропии за счет ее подвода извне будет равно:
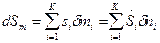 .
.
Для обратимых процессов при подводе теплоты 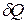 извне изменение энтропии ТС равно изменению энтропии окружающей среды с обратным знаком, т.е.
извне изменение энтропии ТС равно изменению энтропии окружающей среды с обратным знаком, т.е.
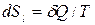 ,
,
а в случае необратимых процессов
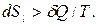
При протекании процессов внутри ТС энтропия может только расти, т.е. dSin >0.
При этом количество энергии упорядоченного движения частиц, которое диссипировало в тепловую энергию, равно: 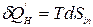 . Тогда математическое выражение второго закона термодинамики для сложной открытой ТС примет вид:
. Тогда математическое выражение второго закона термодинамики для сложной открытой ТС примет вид:
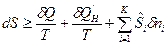 ,
,
где знак «=» для равновесных процессов, а знак «>» для неравновесных процессов.
Знак неравенства показывает, что изменение энтропии больше величины 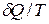 .
.
Для закрытой ТС dSm =0 и математическое выражение 2-го закона термодинамики будет иметь вид:
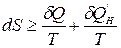 .
.
Для неравновесного кругового процесса
∮ 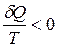 , т.е. круговой интеграл по неравновесному пути не определяет изменение энтропии в круговом процессе (цикле), а меньше его. (Для равновесного кругового процесса ∮
, т.е. круговой интеграл по неравновесному пути не определяет изменение энтропии в круговом процессе (цикле), а меньше его. (Для равновесного кругового процесса ∮ 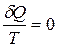 ).
).
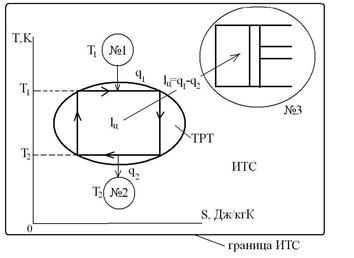
В качестве примера, характеризующего возрастание энтропии при неравновесных процессах, рассмотрим самопроизвольный переход теплоты от горячего тела №1 с температурой Т 1 к холодному телу №2 с температурой Т 2, приведя их в контакт и рассматривая систему из этих тел, как изолированную ТС, в соответствии со следующей схемой:
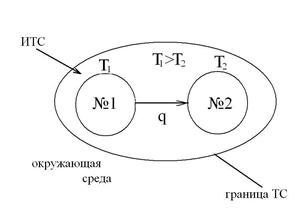
Изменение энтропии этой изолированной ТС будет равна сумме изменений энтропий тел №1 и №2 т.к. энтропия - величина аддитивная:
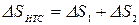 ,
,
или 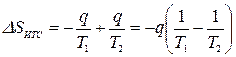 ,
,
где знак минус перед q/T1 означает, что тело №1 отводит теплоту, а знак плюс перед q/T2 означает, что к телу №2 подводится теплота.
Так как Т1>Т2, то 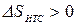 , т.е. в результате неравновесного теплообмена энтропия ИТС возрастает.
, т.е. в результате неравновесного теплообмена энтропия ИТС возрастает.
Для равновесного перехода теплоты от тела №1 к телу №2 необходим посредник – термодинамическое рабочее тело (ТРТ), которое могло бы совершать обратимый цикл Карно, взаимодействуя с телами №1 и №2, как с источником теплоты и холодильником. Тело №3 – аккумулятор работы, который равновесно воспринимает от рабочего тела механическую работу. Тогда 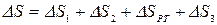 , где
, где 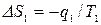 ,
, 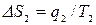 ,
, 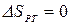 , т.к. совершив цикл, ТС возвращается в исходное состояние, и
, т.к. совершив цикл, ТС возвращается в исходное состояние, и 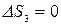 , т.к. тело №3 не участвует в теплообмене.
, т.к. тело №3 не участвует в теплообмене.
Тогда 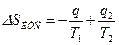 (с учетом знаков, принятых в термодинамике). Для цикла Карно известно, что термический коэффициент полезного действия цикла равен
(с учетом знаков, принятых в термодинамике). Для цикла Карно известно, что термический коэффициент полезного действия цикла равен 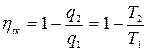 , или
, или 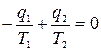 , т.е. сумма приведенных теплот цикла Карно равна нулю. Следовательно, изменение энтропии ИТС
, т.е. сумма приведенных теплот цикла Карно равна нулю. Следовательно, изменение энтропии ИТС 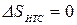 .
.
 2015-01-21
2015-01-21 1728
1728
