 Процесс решения по методу Гаусса состоит из двух этапов.
Процесс решения по методу Гаусса состоит из двух этапов.
На первом этапе система (1) приводится к одной из следующих систем:
· 
 (2)
(2)
где 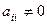 ,
, 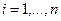 .
.
· 
 (3)
(3)
где 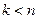 .
.
· 
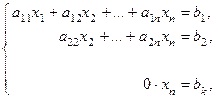 (4)
(4)
 где
где 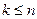 .
.
На втором этапе:
· система (2) имеет единственное решение, значение 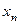 находится из последнего уравнения, значение
находится из последнего уравнения, значение 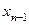 — из предпоследнего,…,значение
— из предпоследнего,…,значение 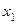 — из первого;
— из первого;
· система (3) имеет бесконечное множество решений;
· система (4) несовместна, так как никакие значения неизвестных не могут удовлетворять её последнему уравнению.
 Метод Гаусса. применим к любой (!) системе линейных уравнений. Метод Гаусса. применим к любой (!) системе линейных уравнений.
|
Опишем метод Гаусса подробнее на примере.
Пример 2.4. Исследуйте систему линейных уравнений примера 2.1; и если она совместна, то найдите её решение: 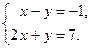
 I. Исследуем систему на совместность. Запишем расширенную матрицу системы и приведём её к ступенчатому виду с помощью элементарных преобразований:
I. Исследуем систему на совместность. Запишем расширенную матрицу системы и приведём её к ступенчатому виду с помощью элементарных преобразований:
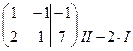 ~
~ 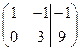 .
.
Очевидно, что 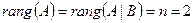 . Значит, согласно (**) (см. §1), система совместна и определённа, т.е. существует единственное решение.
. Значит, согласно (**) (см. §1), система совместна и определённа, т.е. существует единственное решение.
II. Найдём решение системы. Запишем систему уравнений, соответствующую полученной расширенной матрице: 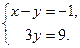 Имеем систему вида (2). Из второго уравнения
Имеем систему вида (2). Из второго уравнения  . Подставляя это значение в первое уравнение, получим:
. Подставляя это значение в первое уравнение, получим: 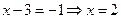 .
.
 Ответ:
Ответ: 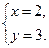
Пример 2.5. Исследуйте систему линейных уравнений примера 2.3, и если она совместна, то найдите её решение: 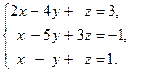
 I. Исследуем систему на совместность. Запишем расширенную матрицу системы и приведём её к ступенчатому виду с помощью элементарных преобразований:
I. Исследуем систему на совместность. Запишем расширенную матрицу системы и приведём её к ступенчатому виду с помощью элементарных преобразований:
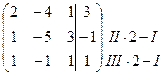 ~
~ 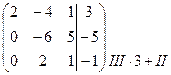 ~
~
~ 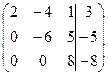 .
.
Очевидно, что 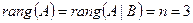 . Значит, согласно (**) (см. §1), система совместна и определённа, т.е. существует единственное решение.
. Значит, согласно (**) (см. §1), система совместна и определённа, т.е. существует единственное решение.
II. Найдём решение системы. Запишем систему уравнений, соответствующую полученной расширенной матрице: 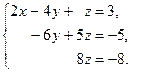
Имеем систему вида (2). Из третьего уравнения 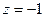 .
.
Подставляя это значение во второе уравнение, получим: 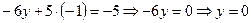 .
.
Подставляя найденные значения 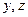 в первое уравнение, получим:
в первое уравнение, получим: 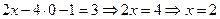 .
.
 Ответ:
Ответ: 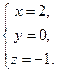
Пример 2.6. Исследуйте систему линейных уравнений, и если она совместна, то найдите её решение: 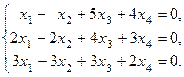
 I. Исследуем систему на совместность. Запишем расширенную матрицу системы и приведём её к ступенчатому виду с помощью элементарных преобразований:
I. Исследуем систему на совместность. Запишем расширенную матрицу системы и приведём её к ступенчатому виду с помощью элементарных преобразований:
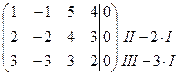 ~
~ 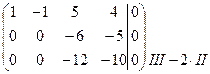 ~~
~~ 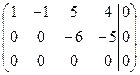 .
.
Очевидно, что 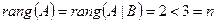 . Значит, согласно (***) (см. §1), система совместна и неопределённа, т.е. имеет бесконечно много решений.
. Значит, согласно (***) (см. §1), система совместна и неопределённа, т.е. имеет бесконечно много решений.
II. Найдём решение системы. Запишем систему уравнений, соответствующую полученной расширенной матрице:
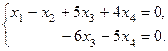
Имеем систему вида (3). Выразим 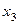 из второго уравнения и подставим полученное выражение в первое уравнение:
из второго уравнения и подставим полученное выражение в первое уравнение:
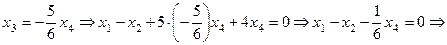
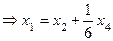 .
.
Следовательно, исходная система имеет решение 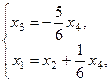 где
где  ,
, 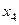 могут принимать любые действительные значения.
могут принимать любые действительные значения.
 Ответ:
Ответ: 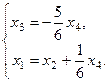
| Продукт | Сырье | |
| I | II | |
| 1,5 | |
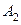
| ||
| Запасы |
Пример 2.7. Цех выпускает два вида продукции 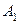 и
и 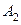 , полностью используя для их производства сырье вида I и вида II. В таблице указано число единиц сырья I и II, необходимых для производства одной единицы продукции
, полностью используя для их производства сырье вида I и вида II. В таблице указано число единиц сырья I и II, необходимых для производства одной единицы продукции 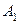 и
и 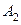 , а также имеющиеся запасы сырья.
, а также имеющиеся запасы сырья.
Может ли цех удовлетворить заказ трёх торговых организаций:
| Продукт | Заказ I организации | Заказ II организации | Заказ III организации |
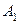
| |||
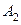
|
 Пусть
Пусть 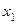 и
и  — количество единиц продукции
— количество единиц продукции 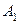 и
и 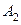 соответственно, которое может выпустить цех при данных условиях производства. Тогда данные первой таблицы можно представить системой уравнений:
соответственно, которое может выпустить цех при данных условиях производства. Тогда данные первой таблицы можно представить системой уравнений: 
Решим её методом Гаусса.
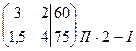 ~
~ 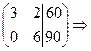
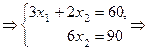
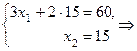
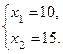
Т.е. цех произведёт 10 единиц продукта 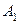 , 15 единиц — продукта
, 15 единиц — продукта 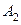 .
.
Выясним, сможет ли цех выполнить заказ.
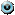 Для выполнения заказа нужно
Для выполнения заказа нужно  единиц продукта
единиц продукта 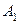 и
и 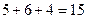 единиц продукта
единиц продукта 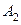 . Следовательно, цех может выполнить заказ.
. Следовательно, цех может выполнить заказ.
 2015-01-21
2015-01-21 564
564








