Пусть задана система из 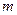 линейных уравнений с
линейных уравнений с 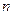 неизвестными
неизвестными 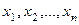 :
:
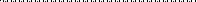
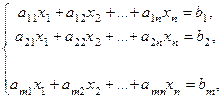 (1)
(1)
 где числа
где числа 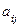 называются коэффициентами системы,
называются коэффициентами системы,

 а числа
а числа 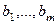 — свободными членами.
— свободными членами.
Решением системы (1) называется такой набор чисел 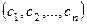 , что при его подстановке в систему вместо соответствующих неизвестных (
, что при его подстановке в систему вместо соответствующих неизвестных (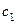 вместо
вместо 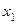 ,…,
,…, 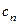 вместо
вместо 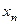 ) каждое из уравнений системы обращается в тождество.
) каждое из уравнений системы обращается в тождество.
 Совместной называется система, которая имеет хотя бы одно решение.
Совместной называется система, которая имеет хотя бы одно решение.

 Несовместной называется система, которая не имеет ни одно го решения.
Несовместной называется система, которая не имеет ни одно го решения.
 Определённой называется система, которая имеет единственное решение.
Определённой называется система, которая имеет единственное решение.
 Неопределённой называется система, которая имеет более одного решения.
Неопределённой называется система, которая имеет более одного решения.
 Однородной называется система, если
Однородной называется система, если 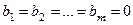 . В противном случае система называется неоднородной.
. В противном случае система называется неоднородной.
Матрицей системы называется матрица, составленная из коэффициентов системы:


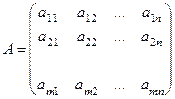 .
.
Расширенной матрицей системы называется матрица


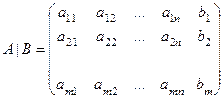 .
.
 Теорема Кронекера-Капелли. Cистема линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы:
Теорема Кронекера-Капелли. Cистема линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы:
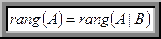

 Исследовать систему линейных уравнений означает определить, совместна она или нет, а для совместной системы — выяснить, определённа она или нет. При этом возможны три варианта:
Исследовать систему линейных уравнений означает определить, совместна она или нет, а для совместной системы — выяснить, определённа она или нет. При этом возможны три варианта:
1) Если 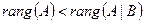 , то система несовместна. (*)
, то система несовместна. (*)

 2) Если
2) Если 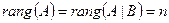 , где
, где 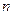 — число неизвестных, то система совместна и определённа. (**)
— число неизвестных, то система совместна и определённа. (**)
3) Если 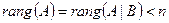 , то система совместна и неопределённа. (***)
, то система совместна и неопределённа. (***)

 § 2. Решение систем линейных уравнений
§ 2. Решение систем линейных уравнений
Метод Крамера
 Пусть система из
Пусть система из 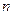 линейных уравнений с
линейных уравнений с 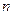 неизвестными записана в матричной форме:
неизвестными записана в матричной форме: 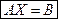 , где
, где 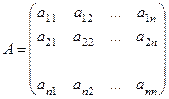 — матрица системы,
— матрица системы,
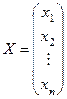 — столбец неизвестных,
— столбец неизвестных, 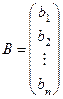 — столбец свободных членов.
— столбец свободных членов.
Пусть 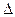 — определитель матрицы
— определитель матрицы 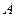 и пусть
и пусть 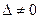 , т.е.
, т.е.

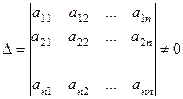
 Правило Крамера. Если определитель системы (1) Правило Крамера. Если определитель системы (1) 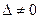 , то эта система совместна и определённа, т.е. имеет единственное решение, получаемое по формулам: , то эта система совместна и определённа, т.е. имеет единственное решение, получаемое по формулам:  , , 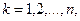 где где 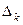 — определитель, получаемый из определителя — определитель, получаемый из определителя 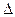 заменой заменой 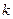 -го столбца на столбец свободных членов. -го столбца на столбец свободных членов. |
Пример 2.1. Решите систему уравнений по формулам Крамера:
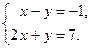
 Найдём определитель матрицы системы:
Найдём определитель матрицы системы: 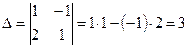 .
.
Т.к. 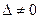 , то решение системы существует и единственно.
, то решение системы существует и единственно.
Найдём определитель 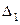 . В определитель
. В определитель 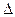 вместо первого столбца
вместо первого столбца 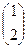 подставим столбец свободных членов
подставим столбец свободных членов 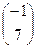 :
:
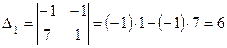 .
.
Определитель 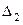 получается из
получается из 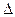 подстановкой столбца свободных членов
подстановкой столбца свободных членов 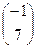 вместо второго столбца
вместо второго столбца 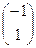 :
:
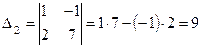 .
.
Отсюда получим решение системы уравнений:
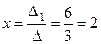 ;
; 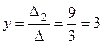 .
.
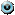 Ответ:
Ответ: 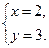
 Матричный метод
Матричный метод
 Пусть система из
Пусть система из 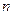 линейных уравнений с
линейных уравнений с 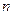 неизвестными записана в матричной форме:
неизвестными записана в матричной форме: 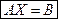 , Тогда, если определитель
, Тогда, если определитель 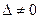 , то система совместна и определённа, её решение задаётся формулой:
, то система совместна и определённа, её решение задаётся формулой:
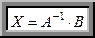
Пример 2.2. Решите систему уравнений примера 2.1 с помощью обратной матрицы: 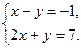 .
.
1)  Т.к.
Т.к. 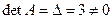 , то решение системы существует и единственно.
, то решение системы существует и единственно.
2) Найдём алгебраические дополнения к элементам матрицы 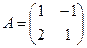 :
: 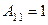 ,
, 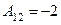 ,
, 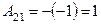 ,
, 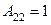 .
.
3) Найдём присоединённую матрицу: 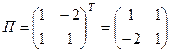 .
.
4) Найдём матрицу 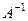 :
: 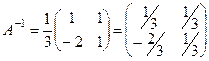 .
.
5) Найдём решение системы уравнений:
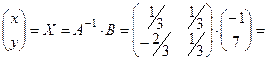
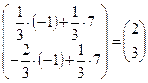 .
.
 Ответ:
Ответ: 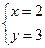 .
.
Пример 2.3. Решите систему уравнений по формулам Крамера и с помощью обратной матрицы: 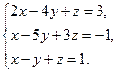
 I способ, метод Крамера.
I способ, метод Крамера.
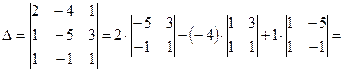
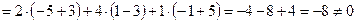 .
.
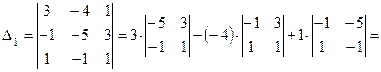
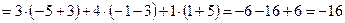 .
.
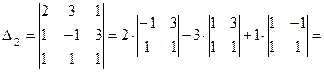
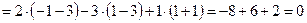 .
.
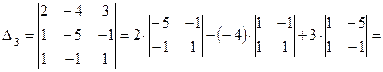
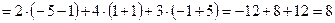 .
.
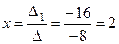 ,
, 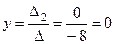 ,
, 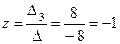 .
.
 Ответ:
Ответ: 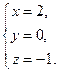
 II способ, метод обратной матрицы.
II способ, метод обратной матрицы.
1) 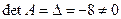 .
.
2) 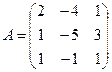
Алгебраические дополнения элементов матрицы 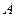 :
:
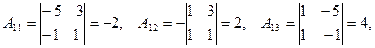
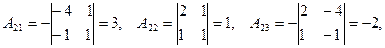
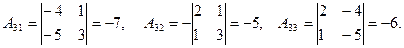
3) Присоединенная матрица:
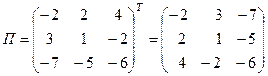 .
.
4) Обратная матрица:
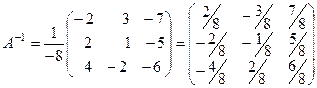 .
.
5) Решение системы:
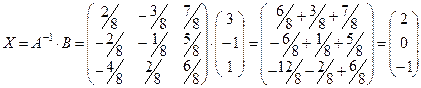 .
.

 Ответ:
Ответ: 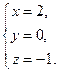
 2015-01-21
2015-01-21 1498
1498








