Рис.4.1
Уравнение Бернулли. Пусть рассматриваемые сечения трубки тока идеальной жидкости малы, так что можно считать величины скорости 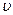 и давления
и давления 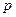 в них постоянными, т.е.
в них постоянными, т.е. 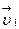 и
и 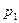 , в сечении
, в сечении 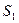 и
и 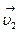 ,
, 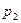 в
в 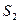 (рис. 4.2).
(рис. 4.2).
При движении жидкости за малый промежуток времени 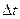 сечение
сечение 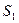 , переместится в положение
, переместится в положение 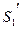 пройдя путь
пройдя путь 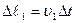 , а сечение
, а сечение 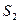 - в положение
- в положение 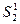 , пройдя
, пройдя 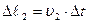 . Объем жидкости, заключенный между сечениями
. Объем жидкости, заключенный между сечениями 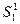 и
и 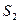 вследствие уравнения неразрывности будет
вследствие уравнения неразрывности будет  равен объем жидкости, заключенному в промежутке
равен объем жидкости, заключенному в промежутке
Рис. 4.2 между 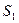 и
и 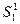 . Трубка имеет некоторый наклон
. Трубка имеет некоторый наклон
и центры ее сечений 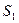 и
и 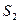 находятся на высотах
находятся на высотах 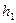 и
и 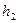 над заданным
над заданным
горизонтальным уровнем. Учитывая, что 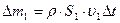 и
и 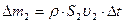 , изменение полной энергии выделенной массы жидкости, расположенной в начальный момент между сечениями
, изменение полной энергии выделенной массы жидкости, расположенной в начальный момент между сечениями 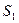 и
и 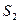 , может быть представлено в виде
, может быть представлено в виде
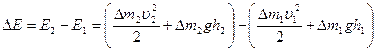 . (4.3)
. (4.3)
Это изменение, согласно закону сохранения энергии, обусловлено работой внешних сил. В данном случае это силы давления 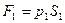 и
и 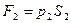
 , действующие, соответственно, на сечения
, действующие, соответственно, на сечения 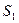 и
и 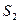 , где
, где 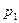 и
и 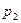 соответствующие давления. Для любого сечения трубки тока
соответствующие давления. Для любого сечения трубки тока
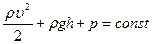 , (4.4)
, (4.4)
где 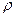 – плотность жидкости Равенство (4.4) выражает основной закон гидродинамики, которое называется также уравнением Бернулли по имени ученого, получившего его впервые.
– плотность жидкости Равенство (4.4) выражает основной закон гидродинамики, которое называется также уравнением Бернулли по имени ученого, получившего его впервые.
Давление в потоке жидкости. Следует отметить, что в выражении (4.4) все слагаемые имеют размерность давления и соответственно называются: 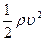 –динамическим,
–динамическим, 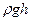 – гидростатическим или весовым,
– гидростатическим или весовым, 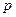 – статическим давлением, а их сумма полным давлением. С учетом этого соотношение (4.4) можно выразить словами: в стационарном течении идеальной жидкости полное давление в любом сечении трубки тока (в пределе- линии тока) – величина постоянная, а скорость потока
– статическим давлением, а их сумма полным давлением. С учетом этого соотношение (4.4) можно выразить словами: в стационарном течении идеальной жидкости полное давление в любом сечении трубки тока (в пределе- линии тока) – величина постоянная, а скорость потока
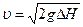 . (4.5)
. (4.5)
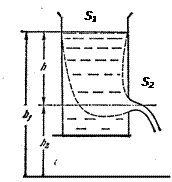
Истечение жидкости из отверстия. Пусть отверстие 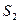 находящееся вблизи дна сосуда заполненного жидкостью, открыто (рис. 4.3). Выделим трубку тока с сечениями
находящееся вблизи дна сосуда заполненного жидкостью, открыто (рис. 4.3). Выделим трубку тока с сечениями 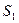 - на уровне
- на уровне 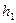 открытой поверхности жидкости в сосуде;
открытой поверхности жидкости в сосуде; 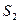 - на уровне отверстия -
- на уровне отверстия - 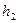 . Для них уравнение Бернулли имеет вид
. Для них уравнение Бернулли имеет вид
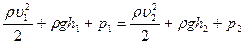 . (4.6)
. (4.6)
 Здесь
Здесь 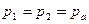 , где
, где 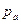 - атмосферное давление. Поэтому из (4.6) имеем
- атмосферное давление. Поэтому из (4.6) имеем
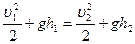 (4.7)
(4.7)
Если 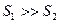 , то
, то 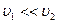 и членом
и членом 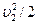 можно
можно
Рис. 4.3 пренебречь. Тогда из (4.7) получим
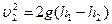 .
.
Следовательно, скорость истечения жидкости будет равна:
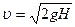 , (4.8)
, (4.8)
где 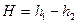 . Формула (4.8) получена впервые Торричелли и носит его имя. За малый промежуток времени
. Формула (4.8) получена впервые Торричелли и носит его имя. За малый промежуток времени 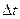 из сосуда вытекает объем жидкости
из сосуда вытекает объем жидкости 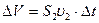 . Соответствующая ему масса
. Соответствующая ему масса 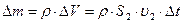 , где
, где 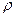 - плотность жидкости. Она имеет импульс
- плотность жидкости. Она имеет импульс 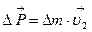 . Следовательно, сосуд сообщает этот импульс вытекающей массе
. Следовательно, сосуд сообщает этот импульс вытекающей массе 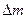 , т.е. действует силой
, т.е. действует силой
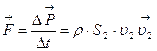 .
.
По третьему закону Ньютона на сосуд будет при этом действовать сила 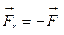 , т.е.
, т.е.
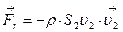 . (4.9)
. (4.9)
Здесь 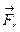 - сила реакции текущей жидкости. Если сосуд находится на тележке, то он под действием силы
- сила реакции текущей жидкости. Если сосуд находится на тележке, то он под действием силы 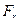 придет в движение, которое называется реактивным движением.
придет в движение, которое называется реактивным движением.
Ламинарное и турбулентное течения. Вязкость. Течение жидкости, при котором каждый ее слой скользит относительно других таких же слоев, и отсутствует их перемешивание, называется ламинарным или слоистым. Если внутри жидкости происходит образование вихрей и интенсивное перемешивание слоев, то такое течение называется турбулентным.
Установившееся (стационарное) течение идеальной жидкости является ламинарным при любых скоростях. В реальных жидкостях между слоями возникают силы внутреннего трения, т.е. реальные жидкости обладают вязкостью. Поэтому, каждый из слоев тормозит движение соседнего слоя. Величина силы внутреннего трения пропорциональна площади соприкосновения слоев 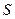 и градиенту скорости
и градиенту скорости 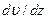 , т.е.
, т.е.
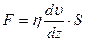 , (4.10)
, (4.10)
где 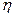 - коэффициент пропорциональности, называемый коэффициентом вязкости. Единицей его является
- коэффициент пропорциональности, называемый коэффициентом вязкости. Единицей его является 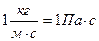 (Паскаль- секунда). Вязкость зависит от рода жидкости и от температуры. С ростом температуры вязкость уменьшается.
(Паскаль- секунда). Вязкость зависит от рода жидкости и от температуры. С ростом температуры вязкость уменьшается.
Если сила внутреннего трения 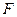 невелика и скорость течения
невелика и скорость течения 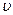 мала, то движение практически является ламинарным. При больших силах внутреннего трения нарушается слоистый характер течения, начинается интенсивное перемешивание, т.е. происходит переход к турбулентности. Условия этого перехода при течении жидкости по трубам определяется величиной
мала, то движение практически является ламинарным. При больших силах внутреннего трения нарушается слоистый характер течения, начинается интенсивное перемешивание, т.е. происходит переход к турбулентности. Условия этого перехода при течении жидкости по трубам определяется величиной 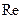 кр, называемой числом Рейнольдса
кр, называемой числом Рейнольдса
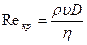 , (4.11)
, (4.11)
где 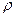 - плотность жидкости,
- плотность жидкости, 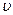 - средняя по сечению трубы скорость течения,
- средняя по сечению трубы скорость течения, 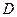 - диаметр трубы. Опыты показывают, что при
- диаметр трубы. Опыты показывают, что при 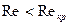 течение ламинарное, при
течение ламинарное, при 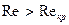 оно становится турбулентным. Для труб круглого сечения радиуса
оно становится турбулентным. Для труб круглого сечения радиуса 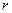 число Рейнольдса
число Рейнольдса 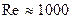 . Влияние вязкости приводит к тому, что при
. Влияние вязкости приводит к тому, что при 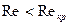 скорость течения по трубе круглого сечения у различных слоев оказывается разной. Ее среднее значение определяется формулой Пуазейля
скорость течения по трубе круглого сечения у различных слоев оказывается разной. Ее среднее значение определяется формулой Пуазейля
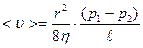 , (4.12)
, (4.12)
где 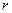 - радиус трубы, (
- радиус трубы, (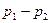 )- разность давлений на концах трубы,
)- разность давлений на концах трубы, 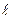 - ее длина.
- ее длина.
Влияние вязкости обнаруживается и при взаимодействии потока с неподвижным телом. Обычно, в соответствии с механическим принципом относительности, рассматривается обратная задача, Например, Стоксом установлено, что при 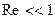 на шар, движущийся в жидкости, действует сила трения
на шар, движущийся в жидкости, действует сила трения
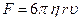 , (4.13)
, (4.13)
где r- радиус шарика, 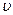 - скорость его движения. Формула Стокса (4.13) в лабораторном практикуме применяется для определения коэффициента вязкости
- скорость его движения. Формула Стокса (4.13) в лабораторном практикуме применяется для определения коэффициента вязкости 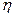 жидкостей.
жидкостей.
Колебания и волны
Колебательным движением, или просто колебанием, называется движение, характеризующееся той или иной степенью повторяемости во времени значений физических величин, определяющих это движение. С колебаниями мы встречаемся при изучении самых различных физических явлений: звука, света, переменных токов, радиоволн, качаний маятника и т.д. Несмотря на большое разнообразие колебательных процессов, все они совершаются по некоторым общим для них закономерностям. Наипростейшее из них- гармоническое колебательное движение. Колебательное движение называется гармоническим, если изменение физической величины х (смещения) происходит по закону косинуса (или синуса)
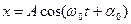 , (4.14)
, (4.14)
где величина А – равная максимальному смещению х системы из положения равновесия, называется амплитудой колебания, (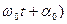 , определяет величину смещения х в данный момент времени
, определяет величину смещения х в данный момент времени 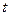 и называется фазой колебания. В момент начала отсчета времени (
и называется фазой колебания. В момент начала отсчета времени (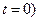 фаза колебания равна
фаза колебания равна 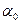 . Поэтому величина
. Поэтому величина 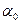 называется начальной фазой. Фаза измеряется в радианах или градусах,
называется начальной фазой. Фаза измеряется в радианах или градусах, 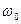 - циклическая частота, равная числу полных колебаний, происходящих за время
- циклическая частота, равная числу полных колебаний, происходящих за время 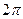 с.
с.
Период - это время одного полного колебания. Он связан с циклической частотой 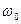 следующим соотношением
следующим соотношением
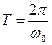 . (4.15)
. (4.15)
Очевидно, линейная частота 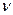 (число колебаний в единицу времени) связана с периодом Т следующим образом
(число колебаний в единицу времени) связана с периодом Т следующим образом
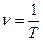 (4.16)
(4.16)
За единицу частоты принимается частота такого колебания, период которого равен 1с. Эту единицу называют герцем (Гц). Частота в 103Гц называется килогерцем (кГц), в 106Гц, мегагерцем (МГц).
Колебательное движение характеризуется не только смещением х, но также скоростью 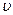 и ускорением а. Их значения могут быть определены из выражения (4.14).
и ускорением а. Их значения могут быть определены из выражения (4.14).
Продифференцировав (4.14) по времени, получим формулу скорости
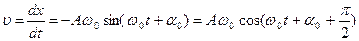 . (4.17)
. (4.17)
Как видно из (4.17), скорость также изменяется по гармоническому закону, причем амплитуда скорости равна 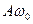 . Из сравнения (4.14) и (4.17) следует, что скорость опережает смещение по фазе на
. Из сравнения (4.14) и (4.17) следует, что скорость опережает смещение по фазе на 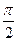 .
.
Продифференцировав (4.14) еще раз по времени, найдем выражение для ускорения
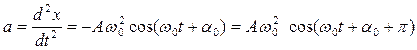 . (4.18)
. (4.18)
Как следует из (4.14) и (4.18), ускорение и смещение находятся в противофазе. Это означает, что в тот момент, когда смещение достигает наибольшего положительного значения, ускорение достигает наибольшего по величине отрицательного значения, и наоборот.
Уравнение плоской бегущей волны
Уравнением волны называется выражение, описывающее зависимость смещения 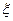 колеблющейся частицы от координат
колеблющейся частицы от координат 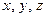 и времени
и времени 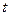 :
:
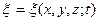 . (4.20)
. (4.20)
Пусть точки, расположенные в плоскости 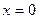 , совершают колебания по закону
, совершают колебания по закону 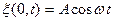 . Колебания частиц среды в точке
. Колебания частиц среды в точке 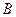 (рис.4.4), расположенной на расстоянии
(рис.4.4), расположенной на расстоянии 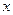 от источника колебаний
от источника колебаний 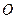 , будут происходить по тому же закону, но, будут отставать по времени от колебаний источника на
, будут происходить по тому же закону, но, будут отставать по времени от колебаний источника на 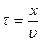 (где
(где 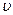 - скорость распространения волны). Уравнение колебания этих частиц имеет вид:
- скорость распространения волны). Уравнение колебания этих частиц имеет вид: 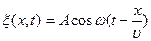 (4.20)
(4.20)
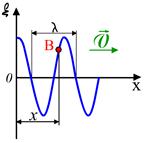 Рис.4.4
Рис.4.4
| Так как точка 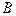 была выбрана произвольно, то уравнение (5.7) позволяет определить смещение любой точки среды, вовлеченной в колебательный процесс, в любой момент времени, поэтому называется уравнением плоской бегущей волны. В общем случае оно имеет вид: была выбрана произвольно, то уравнение (5.7) позволяет определить смещение любой точки среды, вовлеченной в колебательный процесс, в любой момент времени, поэтому называется уравнением плоской бегущей волны. В общем случае оно имеет вид:
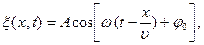 (4.21)
где (4.21)
где 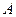 – амплитуда волны; – амплитуда волны; 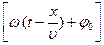 – фаза плоской волны; – фаза плоской волны; 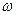 – циклическая частота волны; – циклическая частота волны; 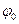 – начальная фаза колебаний. – начальная фаза колебаний.
|
Подставляя в уравнение (4.21) выражения для скорости (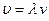 ) и циклической частоты (
) и циклической частоты (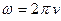 ), получим:
), получим:
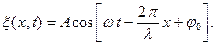 (4.22)
(4.22)
Если ввести волновое число 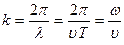 , то уравнение плоской волны можно записать в виде:
, то уравнение плоской волны можно записать в виде:
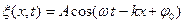 . (4.23)
. (4.23)
Скорость 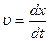 в этих уравнениях представляет собой скорость перемещения фазы волны, и ее называют фазовой скоростью. Действительно, пусть в волновом процессе фаза постоянна
в этих уравнениях представляет собой скорость перемещения фазы волны, и ее называют фазовой скоростью. Действительно, пусть в волновом процессе фаза постоянна 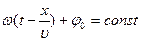 . Для нахождения скорости ее перемещения разделим выражение для фазы на
. Для нахождения скорости ее перемещения разделим выражение для фазы на 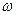 и продифференцируем по времени. Получим:
и продифференцируем по времени. Получим:
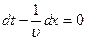 , откуда
, откуда 
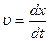 .
.
Стоячая волна. Если в среде одновременно распространяется несколько волн, то выполняется принцип суперпозиции (наложения): каждая волна ведет себя так, как будто другие волны отсутствуют, а результирующее смещение частиц среды в любой момент времени равно геометрической сумме смещений, которые получают частицы, участвуя в каждом из слагающих волновых процессов.
Большой практический интерес представляет наложение двух плоских волн
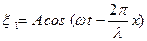 и
и 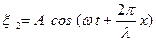 , (4.24)
, (4.24)
с одинаковыми частотами 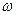 и амплитудами
и амплитудами 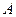 , распространяющихся навстречу друг другу вдоль оси
, распространяющихся навстречу друг другу вдоль оси 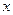 . Сложив эти уравнения, получим уравнение результирующей волны, называемой стоячей волн
. Сложив эти уравнения, получим уравнение результирующей волны, называемой стоячей волн 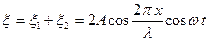 . (4.25)
. (4.25)
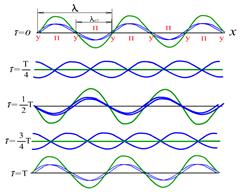 Рис.4.5
Рис.4.5
| Амплитуда стоячей волны 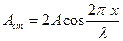 (4.26) является периодической функцией координаты (4.26) является периодической функцией координаты  и не зависит от времени.
В точках среды, где и не зависит от времени.
В точках среды, где 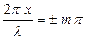  , амплитуда волны достигает максимального значения ( , амплитуда волны достигает максимального значения (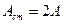 ). Эти точки называются пучностями ( ). Эти точки называются пучностями (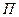 ) стоячей волны. Координаты пучностей ) стоячей волны. Координаты пучностей 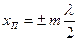 . .
|
Таблица 4.1
В бегущей волне
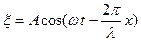
| В стоячей волне
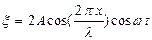
|
| Амплитуда колебаний | |
Все точки среды колеблются с одинаковыми амплитудами 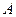
| Все точки среды колеблются с разными амплитудами 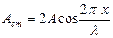
|
| Фаза колебаний | |
Фаза колебаний 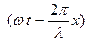 зависит от координаты зависит от координаты 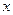 рассматриваемой точки рассматриваемой точки
| Все точки между двумя узлами колеблются в одинаковой фазе 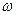 . При переходе через узел фаза колебаний изменяется на . При переходе через узел фаза колебаний изменяется на 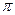 . .
|
| Перенос энергии | |
| Энергия колебательного движения переносится в направлении распространения волны. | Переноса энергии нет, лишь в пределах 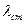 происходят взаимные превращения энергии. происходят взаимные превращения энергии.
|
В точках среды, где 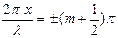
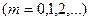 амплитуда волны обращается в ноль (
амплитуда волны обращается в ноль (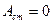 ). Эти точки называются узлами (
). Эти точки называются узлами (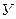 ) стоячей волны. Координаты узлов
) стоячей волны. Координаты узлов 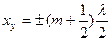 .
.
Расстояние между двумя соседними узлами (или между двумя соседними пучностями), называемое длиной стоячей волны, равно половине длины 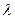 бегущей волны
бегущей волны 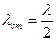 . Таким образом, при сложении двух бегущих волн образуется стоячая волна, узлы и пучности которой находятся все время в одних и тех же местах.
. Таким образом, при сложении двух бегущих волн образуется стоячая волна, узлы и пучности которой находятся все время в одних и тех же местах.
Характеристики бегущей и стоячей волн приведены в табл.5.1.
Осн. 1 [99-101, 108-116 ], 5 [48-54]. 6 [36-46 ]
Доп. 18 [129-157], 22 [ 25-44]
Контрольные вопросы:
Осн. 1 [131-152 ], 8 [56-66 ].
Контрольные вопросы:
1. Может ли быть одинаковым давление в двух точках, лежащих на разных уровнях в установленной наклонно сужающейся трубке, по которой течет идеальная жидкость?
2. Почему струя жидкости, вытекающая из отверстия, по мере удаления от отверстия все больше сжимается?
3.Как соотносятся фазы колебания ускорения и смещения при гармонических колебаниях.
 2015-01-21
2015-01-21 479
479






