Фазу выполнения программы от начала до завершения будем называть запуском. Все возможные результаты запуска разобьем на два класса: правильные и неправильные (ошибочные). Будем считать, что любой результат всегда можно отнести к одному из этих классов. Рассмотрим классическую вероятностную модель последовательности испытаний Бернулли. Пространство элементарных событий в этой модели содержит 2 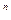
где n - число испытаний (в данном случае под испытанием подразумевается запуск программы). Каждый запуск программы имеет два исхода: правильный и неправильный. Обозначим вероятность неправильного исхода р, а вероятность правильного - (1-р). Вероятность того, что из n запусков К приведут к неправильному результату, выражается хорошо известной формулой биномиального распределения ().
B(p,n,k) = C(n,k) * pk * (1-p)(n-k), (1)
где C(n,k) - число сочетаний. Вероятность P априори неизвестна, но по результатам запусков известны n и K. Величина В как функция P имеет максимум при
р = k/n. (2)
В качестве меры надежности программы можно принять величину
R =1 - k/n = (n-k)/n, (3)
значения которой (от 0 до 1) согласуются с общепринятым смыслом термина надежность: например, если все запуски окончились с ошибочным результатом (к = n), то надежность - нулевая.
Наиболее существенное предположение в данной модели состоит в том, что запуски программы считаются независимыми. Это означает, что результаты предыдущих запусков не дают никакой информации о результатах следующего. Ясно, что это предположение на практике выполняется не всегда: например, повторный запуск с теми же входными данными даст, очевидно, тот же самый результат.
Некоторые следствия. Формула (3) позволяет оценить надежность программы по результатам ее запусков. Следует особо остановиться на двух предельных случаях: K = n (нулевая надежность) и K = 0 (абсолютная надежность). В обоих случаях результаты не следует
интерпретировать буквально.
Если нулевая надежность свидетельствует о том, что программа явно непригодна для эксплуатации, то показатель абсолютной надежности не должен вводить в заблуждение: такой вывод нельзя делать по результатам даже очень большого числа запусков.
Из формулы (3) следует, что оценка надежности программы растет с увеличением числа ее запусков по гиперболическому закону. Это подтверждает интуитивно ясное соображение о том, что программа тем надежнее, чем больше опыт ее эксплуатации, который зависит как от интенсивности использования программы, так и от тиража компьютера, на котором она запускается. Таким образом, надежность программ для персональных компьютеров типа IBM PC, общий тираж которых составляет в настоящее время около 100 миллионов, на несколько порядков выше аналогичных программ для специализированных процессоров (если, конечно, такие программы действительно существуют и эксплуатируются).
Перед пользователем программы, в которого проявились ошибки, возникает дилемма: продолжать ее эксплуатировать или установить модифицированную версию (разумеется, речь не идет о тех случаях, когда последствия ошибок могут быть катастрофическими). Следует еще раз подчеркнуть, что если программа подвергалась модификациям (в частности, в ней исправлялись ошибки), то при оценке надежности следует учитывать только запуски, выполненные с момента последней модификации: в результате модификации получается новая программа, с другим (возможно, худшим) показателем надежности, и вся прежняя статистика должна быть аннулирована. Этим частично объясняется тот факт, что пользователи порой предпочитают обновленным версиям программ старые, проверенные, эксплуатировавшиеся длительное время, даже если в них обнаружены погрешности: опыт эксплуатации стоит очень дорого, и даже если в программе выявлены ошибки, гораздо дешевле внести исправления и дополнения в инструкции к программе (если это, конечно, возможно), чем пожертвовать накопленным опытом.
Интересно сравнить характеристики надежности аппаратуры и компьютерной программы. Как известно, надежность физического устройства меняется со временем: в начале эксплуатации она растет (присходит "приработка" изделия), затем некоторое время остается постоянной и, наконец, начинает уменьшаться (эффект износа или "старения"). Говоря о надежности аппаратуры, имеют в виду именно среднюю фазу, на которой надежность постоянна. Всеми отмечается тот факт, что компьютерная программа не изнашивается, так что последней фазы для нее не существует, однако важно подчеркнуть, что первая фаза ("приработки" программы) тоже отсутствует: коррекция программы (независимо от причин, по которым она выполнялась) аналогична внесению изменений в конструкцию физического устройства, в результате чего получается новое устройство, с другим показателем надежности.
6.6. Модели надежности программного обеспечения
Введение
В области надежности аппаратуры достигнут определенный уровень, когда уже создан ряд математических методов, позволяющих инженеру предсказывать надежность его продукта. Эти математические методы (главным образом в форме вероятностных моделей) широко применяются во многих инженерных областях с такими различными целями, как определение вероятности успешного запуска космического корабля или оценка срока службы устройства для отображения информации. Так как теория надежности аппаратуры развита довольно хорошо, естественно попытаться применить ее и к надежности программного обеспечения.
Для прогнозирования надежности пользуемого программного обеспечения могут применяться различные модели надежности [1].
В моделях надежности программного обеспечения используется информация о числе ошибок, устраненных в процессе тестирования программных средств. На основе такой информации определяются параметры модели и показатели надежности.
Показателем надежности программного обеспечения пожжет служить вероятность отсутствия программных ошибок в течение определенного интервала времени при эксплуатации программы в расчетном режиме на соответствующей вычислительной машине.
Из всех неизвестных показателей надежности программного обеспечения, вероятно, самым важным является число ошибок, оставшихся в программе. Если бы разумная его оценка была известна при тестировании, это помогло бы решить, когда можно закончить процесс. Если знать число оставшихся ошибок в устанавливаемой системе, можно было бы оценить стоимость работ по сопровождению и определить уровень доверия к программе. Другие параметры, для которых желательно иметь оценки,— это надежность программы (вероятность, что программа будет выполняться в течение данного интервала времени, прежде чем обнаружится ошибка заданной степени серьезности) и среднее время между отказами программы.
В настоящей работе рассматривается модель надежности, которая тесно связана с теорией надежности аппаратуры и опирается на определенные предположения о распределении вероятности отказов программного обеспечения.
Модель Джелинского- Моранды
Вероятно, самой известной моделью надежности является модель, разработанная Джелинским и Морандой [1].
Один из способов оценки показателей надежности – наблюдение за поведением программы в течение некоторого периода времени и нанесение на график значений времени между последовательными обнаруженными ошибками.

Рис. 1. Моменты отказов программы на оси времени
Пусть на оси времени в моменты 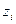 ,
, 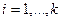 наблюдались события (Рис.1), соответствующие моментам обнаружения ошибок в программе. Интервалы времени между моментами появления событий обозначим символами
наблюдались события (Рис.1), соответствующие моментам обнаружения ошибок в программе. Интервалы времени между моментами появления событий обозначим символами 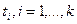 . Они определяются по формуле
. Они определяются по формуле 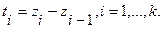
Можно надеяться, что при этом будет обнаружено явление роста надежности: по мере того как ошибки обнаруживаются и исправляются, время между последовательными ошибками становится больше. Экстраполируя эту кривую в будущее, можно предсказать значение 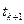 и предсказать полное число ошибок. Такая экстраполяция, однако, в слишком большой степени основана на догадках и обычно уводит в сторону. Было бы лучше опираться на какое-то априорное представление об имеющемся распределении вероятностей ошибок, затем использовать сведения о найденных ошибках для оценки параметров этого распределения и только потом использовать эту модель для предсказания событий в будущем.
и предсказать полное число ошибок. Такая экстраполяция, однако, в слишком большой степени основана на догадках и обычно уводит в сторону. Было бы лучше опираться на какое-то априорное представление об имеющемся распределении вероятностей ошибок, затем использовать сведения о найденных ошибках для оценки параметров этого распределения и только потом использовать эту модель для предсказания событий в будущем.
Разработка такой модели начинается с уточнения поведения функции 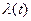 . В большинстве моделей аппаратного обеспечения
. В большинстве моделей аппаратного обеспечения 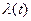 сначала уменьшается со временем (этап, когда обнаруживаются и исправляются ошибки проектирования и производства). Затем она остается постоянной в течение большей части срока службы системы (соответствует случайным отказам) и в конце полезного срока службы системы увеличивается. В теории надежности аппаратуры в основном рассматривается средний период, где функция интенсивности отказов постоянна и потому имеет место соотношение
сначала уменьшается со временем (этап, когда обнаруживаются и исправляются ошибки проектирования и производства). Затем она остается постоянной в течение большей части срока службы системы (соответствует случайным отказам) и в конце полезного срока службы системы увеличивается. В теории надежности аппаратуры в основном рассматривается средний период, где функция интенсивности отказов постоянна и потому имеет место соотношение 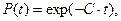 где
где 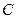 — некоторая константа.
— некоторая константа.
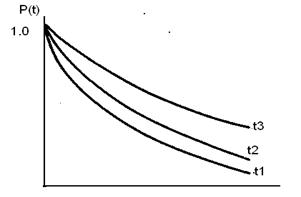
Однако предположение о постоянстве интенсивности обнаружения ошибок в случае программного обеспечения представляется не соответствующим реальности. Для него эта функция должна уменьшаться по мере обнаружения и исправления ошибок. Поэтому, как показано на рис.2,
|
программное обеспечение характеризуется не единственной кривой 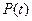 , а их семейством. После каждой обнаруженной ошибки функция
, а их семейством. После каждой обнаруженной ошибки функция 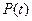 видоизменяется (улучшается).
видоизменяется (улучшается).
Обозначим через 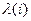 интенсивность потока событий. Будем предполагать:
интенсивность потока событий. Будем предполагать:
1. Случайные величины 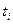 имеют экспоненциальное распределение.
имеют экспоненциальное распределение.
2. Интенсивность потока событий 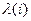
 меняется скачком на
меняется скачком на
3. единицу при возникновении очередного события.
4. События различных типов проявляются с одинаковыми закономерностями.
Выражение для интенсивности имеет следующий вид [2]:
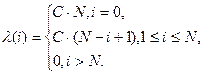 (1)
(1)
где 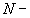 предполагаемое исходное число ошибок в программе,
предполагаемое исходное число ошибок в программе, 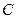 –коэффициент пропорциональности, имеющий физический смысл интенсивности обнаружения единственной ошибки в программе. Его размерность обратно пропорциональна размерности времени. Таким образом, параметр
–коэффициент пропорциональности, имеющий физический смысл интенсивности обнаружения единственной ошибки в программе. Его размерность обратно пропорциональна размерности времени. Таким образом, параметр 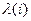 имеет убывающую ступенчатую форму (Рис. 3).
имеет убывающую ступенчатую форму (Рис. 3).
Первое существенное предположение состоит в том, что значение 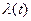 постоянно в течение времени между сбоями, т.е. до обнаружения и исправления очередной ошибки. После этого
постоянно в течение времени между сбоями, т.е. до обнаружения и исправления очередной ошибки. После этого 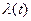 опять становится константой, но уже с другим, меньшим, значением.
опять становится константой, но уже с другим, меньшим, значением. 
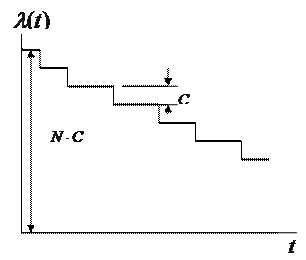
Рис.3. Предполагаемое изменение интенсивности обнаружения ошибок
Второе предположение состоит в том, что интенсивность 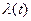 прямо пропорциональна числу оставшихся ошибок, т. е. что
прямо пропорциональна числу оставшихся ошибок, т. е. что 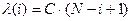 .
.
Каждый раз, когда ошибка обнаруживается (модель предполагает, что задержка между обнаружением ошибки и ее исправлением отсутствует), 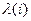 уменьшается на некоторую величину
уменьшается на некоторую величину 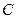 .
.
Определение показателей надежности
Определим показатели надежности программы, имея в виду следующие допущения:
1.Случайные величины 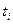 имеют экспоненциальное распределение.
имеют экспоненциальное распределение.
2.Интенсивность отказов 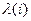 меняется скачком при возникновении и устранении очередной ошибки.
меняется скачком при возникновении и устранении очередной ошибки.
3.Ошибки различных типов проявляются с одинаковыми закономерностями.
4.Отыскание дефекта, приведшего к отказу программы, и его устранение осуществляется мгновенно.
5.В процессе устранения ошибки в программу не вносится новый дефект.
Можно заметить сходство решаемой задачи с задачей определения показателей надежности технической системы с постоянно включенным нагруженным резервом. Ниже приведены рассуждения, подтверждающие это предположение.
Техническая система состоит из 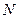 одинаковых подсистем, которые включены между собой параллельно. Поле отказа одной из подсистем она исключается из состава системы. Этот процесс продолжается до момента отказа последней из подсистем, т.е. техническая система постепенно деградирует. В начале тестирования программа может содержать
одинаковых подсистем, которые включены между собой параллельно. Поле отказа одной из подсистем она исключается из состава системы. Этот процесс продолжается до момента отказа последней из подсистем, т.е. техническая система постепенно деградирует. В начале тестирования программа может содержать 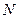 ошибок. После выявления одной из ошибок она исправляется и исключается из состава ошибок. Процесс продолжается до момента обнаружения и исправления последней ошибки из
ошибок. После выявления одной из ошибок она исправляется и исключается из состава ошибок. Процесс продолжается до момента обнаружения и исправления последней ошибки из 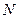 ошибок. Принято считать, что после этого момента времени программа становится абсолютно надежной.
ошибок. Принято считать, что после этого момента времени программа становится абсолютно надежной.
В начале эксплуатации технической системы общая интенсивность отказов ее подсистем прямо пропорциональна их числу, т.е. 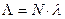 , где
, где 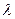
 - интенсивность отказа одной подсистемы. После отказа одной подсистемы общая интенсивность отказов уменьшается, т.е.
- интенсивность отказа одной подсистемы. После отказа одной подсистемы общая интенсивность отказов уменьшается, т.е. 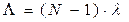
 и т. д. Ясно, что закон изменения интенсивности технической системы аналогичен закономерности (6), принятой для программы. В соответствии с этим определим количественные характеристики надежности программы.
и т. д. Ясно, что закон изменения интенсивности технической системы аналогичен закономерности (6), принятой для программы. В соответствии с этим определим количественные характеристики надежности программы.
Вероятность безошибочной работы за время 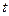 при условии, что до начала этого интервала в программе выявлено и устранено
при условии, что до начала этого интервала в программе выявлено и устранено 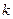 ошибок:
ошибок:
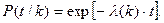 . (2)
. (2)
Отсчет времени в этой формуле начинается от последнего 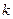 - ого отказа программы.
- ого отказа программы.
Средняя наработка на ошибку при условии, что выявлено 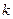 ошибок:
ошибок:
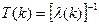 .
.  (3)
(3)
Плотность вероятности длительности безошибочной работы программы при условии, что выявлено и устранено 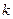 ошибок определяется в соответствии с формулами (1) и (7):
ошибок определяется в соответствии с формулами (1) и (7):
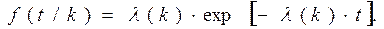 (4)
(4)
Вероятность устранения всех ошибок программы. Представим исходную программу, содержащую 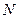 ошибок, в виде
ошибок, в виде 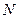 «одинаковых» программ декомпозиции, в каждой из которых содержится ровно одна ошибка, причем одиночные ошибки в разных программах не могут быть одинаковыми. Этот прием позволяет свести решение задачи к определению вероятности отказа технической систем с нагруженным резервом. Известно, что резервированная система откажет, если совместно за время
«одинаковых» программ декомпозиции, в каждой из которых содержится ровно одна ошибка, причем одиночные ошибки в разных программах не могут быть одинаковыми. Этот прием позволяет свести решение задачи к определению вероятности отказа технической систем с нагруженным резервом. Известно, что резервированная система откажет, если совместно за время 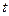 откажет все подсистемы. Аналогично можно утверждать, что в исходной программе будут отсутствовать ошибки, если они будут обнаружены и устранены во всех экземплярах программ декомпозиции.
откажет все подсистемы. Аналогично можно утверждать, что в исходной программе будут отсутствовать ошибки, если они будут обнаружены и устранены во всех экземплярах программ декомпозиции.
Вероятность того, что за время 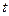 в одном экземпляре программы будет обнаружена и исправлена ошибка
в одном экземпляре программы будет обнаружена и исправлена ошибка
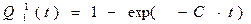 . (5)
. (5)
Определим вероятность обнаружения и исправления за время 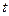 любых
любых 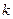 ошибок в программе из
ошибок в программе из 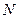 возможных при условии, что остальные
возможных при условии, что остальные 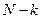 ошибок не обнаружены:
ошибок не обнаружены:
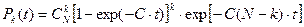 . (6)
. (6)
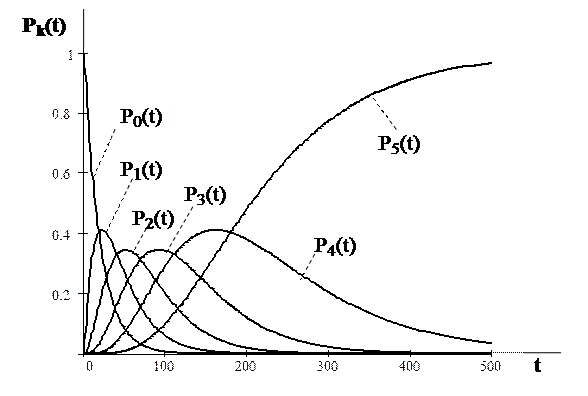
Рис. 4. Графики функций 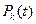
Вероятность устранения за время 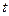 всех ошибок программы:
всех ошибок программы:
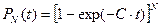 . (7)
. (7)
Вероятность не устранения за время 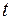 всех ошибок программы:
всех ошибок программы:
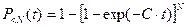 . (8)
. (8)
Средняя длительность интервала времени, за который могут быть устранены все ошибки программы:
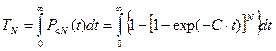 .
.
Введя новую переменную 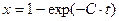 и интегрируя
и интегрируя
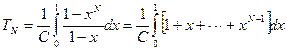
получаем

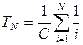 . (9)
. (9)
На рис. 4 показано семейство графиков функций 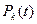 для
для 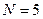 . Используя, например график функции
. Используя, например график функции 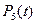 можно определить вероятность обнаружения всех пяти ошибок в течение заданного времени
можно определить вероятность обнаружения всех пяти ошибок в течение заданного времени 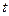 .
.
Марковские модели
Марковская модель основана на том, что программа в процессе тестирования проходит через последовательность состояний (Рис. 5):
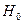 - в программе не обнаружено ни одной ошибки (
- в программе не обнаружено ни одной ошибки (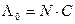 );
);
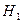 - в программе обнаружена одна ошибка
- в программе обнаружена одна ошибка 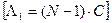 и т. д.;
и т. д.;
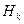 - в программе обнаружено
- в программе обнаружено 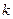 ошибок
ошибок 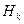
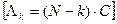 .
.

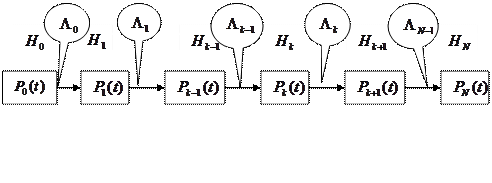
Рис. 5. Граф состояний программы
Методика расчета показателей надежности сводится к следующему правилу:
· составляется система дифференциальных уравнений в соответствии с графом состояний программы;
· выбираются начальные условия решения задачи;
· определяются показатели надежности программы.
Система дифференциальных уравнений составляется согласно правилу: производная вероятности данного состояния равна алгебраической сумме произведений интенсивностей всех возможных переходов этого состояния на вероятность состояний, из которых выходят линии перехода. Знак у слагаемого положительный, если линия перехода входит в данное состояние, и отрицательный, если линия перехода выходит из этого состояния.
Согласно этому правилу составим систему дифференциальных уравнений:
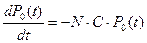 ;
;
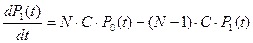 ;
;
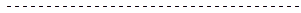
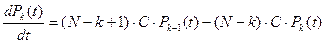 ,
, 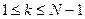 ; (10)
; (10)
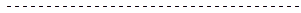
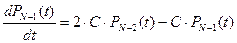 ;
;
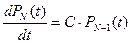 .
.
Система дифференциальных уравнений (10) называется системой уравнений Колмогорова или системой уравнений массового обслуживания.
Необходимо отметить, что состояния программы в момент времени 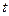 образуют полную группу несовместных состояний. Тогда сумма вероятностей этих состояний
образуют полную группу несовместных состояний. Тогда сумма вероятностей этих состояний

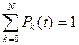 . (11)
. (11)
Выберем начальные условия. В этой задаче они задаются следующими значениями: при 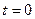 вероятность
вероятность 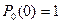 и
и 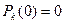 для
для 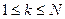 .
.
Систему (10) можно решить с помощью различных программных инструментальных средств. Однако мы покажем возможность использования преобразований Лапласа:
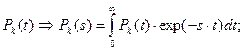 (12)
(12)
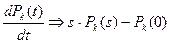 .
.  (13)
(13)
Преобразования Лапласа для уравнений (10) имеют вид:
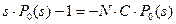 ;
;
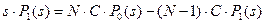 ;
;
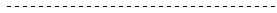
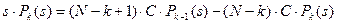 ;
;
(14)
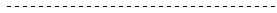
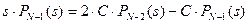 ;
;
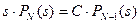 .
.
Рассмотрим способ определения вероятностей различных состояний программы. С начала из первого уравнения системы (14) находим изображение 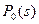 , а затем по таблице преобразования Лапласа определяем оригинал
, а затем по таблице преобразования Лапласа определяем оригинал 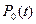 :
:
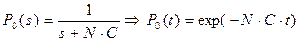 . (15)
. (15)
Из второго уравнения системы находим
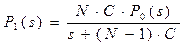 , (16)
, (16)
а затем, подставив в (16) 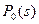 имеем
имеем
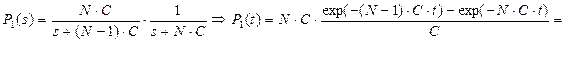
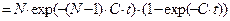 . (17)
. (17)
Аналогичный результат можно получить из соотношения (6) если положить в нем 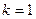 . Операторным методом можно определить функции
. Операторным методом можно определить функции 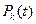 для всех остальных состояний программы.
для всех остальных состояний программы.
Рассмотрим видоизмененный способ решения этой задачи.
Из системы уравнений (14) определяем
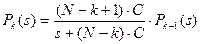 ,
, 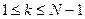 . (18)
. (18)
В соответствии с этим выражением можно ввести в рассмотрение преобразующую систему с передаточной функцией
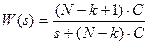 (19)
(19)
и импульсной переходной функцией
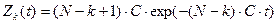 . (20)
. (20)
Эта система - апериодическое звено, которое преобразует входной сигнал 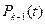 в выходной сигнал
в выходной сигнал 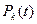 (Рис. 5).
(Рис. 5).
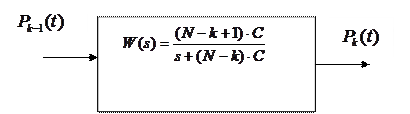
Рис. 6. Преобразующая система
Сигнал на выходе системы определяется в виде интеграла свертки
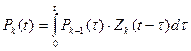 .
.  (21)
(21)
Например, используя формулы (15) и (20), для значения 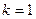 определяем выражение
определяем выражение
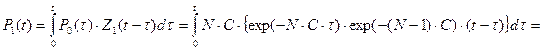
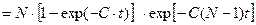 ,
,
которое аналогично результату (17).
Затем, выполняя последовательно свертки, находим выражения 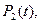
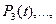
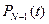 .
.
Из последнего уравнения системы (14) следует
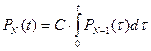 .
.
Определим среднее время нахождения программы в каждом состоянии. Для этого умножим левую и правую часть дифференциальных уравнений системы (10) на 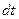 и проинтегрируем их по времени с пределами от
и проинтегрируем их по времени с пределами от 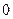 до
до 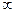 (последнее уравнение не используется, потому что оно соответствует поглощающему состоянию).
(последнее уравнение не используется, потому что оно соответствует поглощающему состоянию).
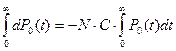 ;
;
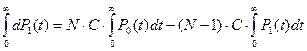 ;
;
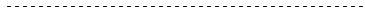
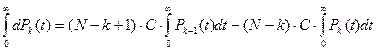 ;
;
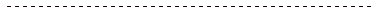

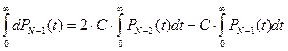 .
.
Учитывая, что 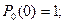
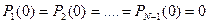 ;
; 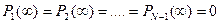 получаем
получаем
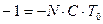 ;
;
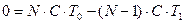 ;
;
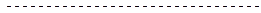
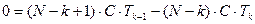 ;
;
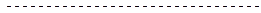
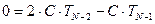 .
.
Решая систему, получаем следующие результаты:
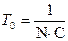 ;
; 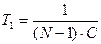 ;
; 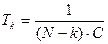 ;
; 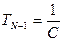 . (22)
. (22)
Определение параметров модели
Итак, выше приведены соотношения, с помощью которых можно рассчитать основные количественные характеристики надежности программы. Для определения значений этих показателей необходимо найти оценки величин 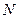 и
и 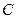 .
.
Рассмотрим несколько методов решения этой задачи.
Метод наименьших квадратов. Предположим, что при отладке программы в моменты времени 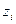 ,
, 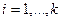 в ней были обнаружены
в ней были обнаружены 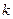 ошибок, т.е. нам известны интервалы времени
ошибок, т.е. нам известны интервалы времени 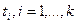 , длина каждого из которых зависит от параметров
, длина каждого из которых зависит от параметров 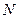 и
и 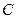 . Очевидно, что интенсивность обнаружения первой ошибки
. Очевидно, что интенсивность обнаружения первой ошибки 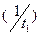 должна быть прямо пропорциональна общему числу ошибок в программе
должна быть прямо пропорциональна общему числу ошибок в программе 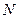 ; интенсивность обнаружения второй ошибки
; интенсивность обнаружения второй ошибки 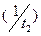 должна быть прямо пропорциональна числу оставшихся ошибок в программе, т.е.
должна быть прямо пропорциональна числу оставшихся ошибок в программе, т.е. 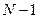 и т. д. Сумма квадратов отклонений теоретических и экспериментальных данных
и т. д. Сумма квадратов отклонений теоретических и экспериментальных данных
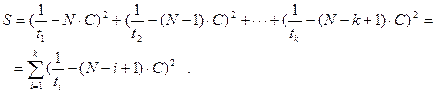 (23)
(23)
Условия нахождения экстремума:
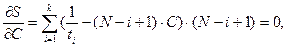 (24)
(24)
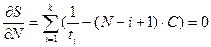 . (25)
. (25)
Пример1. Пусть в ходе отладки зафиксированы интервалы времени 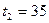
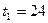 , и
, и 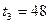 между отказами программы. Необходимо определить параметры
между отказами программы. Необходимо определить параметры 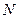 и
и 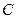 .
.
Из (24) и (25) получим
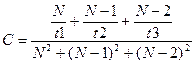 ,
,
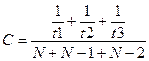 .
.

Составляем уравнение
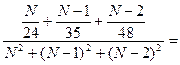
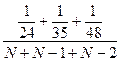 (26)
(26)
и находим значение 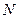 методом перебора.
методом перебора.
Если 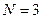 , то в левой части (26) имеем
, то в левой части (26) имеем
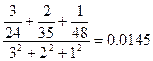 ,
,
а в правой части:
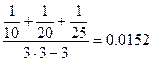 .
.
Если 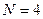 , левая и правая части соответственно равны
, левая и правая части соответственно равны 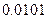 и
и 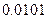 . Если
. Если 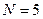 – соответственно
– соответственно 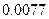 и
и 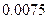 . Следовательно, наименьшую ошибку при решении обеспечит
. Следовательно, наименьшую ошибку при решении обеспечит 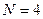 . Таким образом
. Таким образом
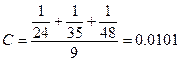 .
.
Метод максимума правдоподобия [2].Функция правдоподобия определяется в виде произведения функцийплотностей вероятности (4) соответствующих различным значениям индекса:
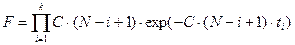 . (27)
. (27)
Для получения оценок 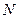 и
и 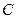 необходимо взять частные производные по неизвестным, приравнять их нулю и решить полученную систему уравнений. Однако, удобнее предварительно прологарифмировать выражение (27):
необходимо взять частные производные по неизвестным, приравнять их нулю и решить полученную систему уравнений. Однако, удобнее предварительно прологарифмировать выражение (27):
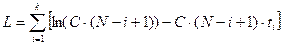 . (28)
. (28)
Условия для нахождения экстремума:

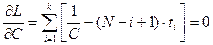 (29)
(29)
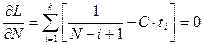 (30)
(30)
Из соотношения (30) получим
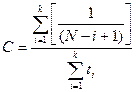 . (31)
. (31)
Из нелинейного уравнения, полученного подстановкой 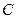 из (31) в (29):
из (31) в (29):
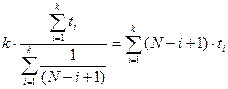 , (32)
, (32)
определяем значение 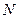 методом перебора.
методом перебора.
Пример 2. Воспользуемся исходными данными примера 1. Если 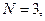 то в левой части (32) имеем
то в левой части (32) имеем 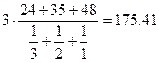 , а в правой части:
, а в правой части: 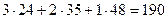 . Если
. Если 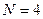 , то левая и правая части уравнения соответственно равны
, то левая и правая части уравнения соответственно равны 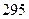 и
и 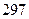 . Если
. Если 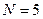 – соответственно
– соответственно 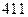 и
и 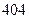 . Следовательно, наименьшую ошибку при решении (36) обеспечивает
. Следовательно, наименьшую ошибку при решении (36) обеспечивает 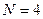 , поэтому из (31) находим
, поэтому из (31) находим

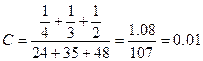 .
.
 2015-01-22
2015-01-22 2458
2458
