2015-01-22
435
Рассмотрим методику расчета момента обнаружения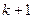 
ошибки [2]. Составим функцию правдоподобия. Введем дополнительный индекс для различения предыдущей и новой функций, а именно, обозначим их как 
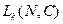и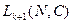 
Тогда можно записать:
(33)
где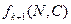 
- плотность вероятности длительности 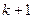интервала до будущей ненаблюдаемой ошибки. Представим ее в виде:
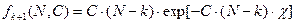(34)
где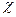 
есть искомая длительность времени от 
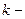го до 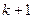- го события.
Прологарифмируем (33) и возьмем частные производные по параметрам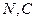 
. Получим следующую систему уравнений:
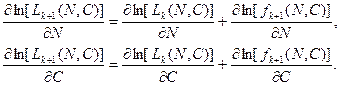(35)
Заметим, что параметры 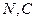определены только для функции 
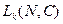, для функции 
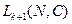они являются приближенными. Приравняем производные от логарифмов функций правдоподобия в обеих частях равенств () к нулю на основании их свойств. Тогда очевидно, что производные
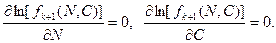(36)
Подставляя (34) в любое из уравнений (36) находим прогностическую оценку момента обнаружения 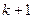ошибки
.
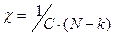Пример3. Используя исходные данные и результаты примера 2 (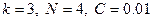
) получим
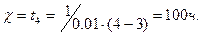
Получив значение 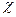, можно с помощью функции правдоподобия 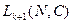уточнить оценки 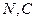и по ним сделать новый прогноз и т.д.
