Перечень вопросов к практическим занятиям по биологии на осенний семестр

1) Введение.

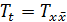(1)

t=0: T=0 (2)

x=0: T[0]=0 (3)

x=1: T[N]= 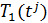(4)

Уравнения (1)-(4) составляют систему, которая на каждом временном слое j представляет собой СЛАУ.

Распишем СЛАУ

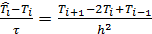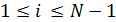, (5)

.

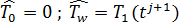Конечно разностная схема (5) содержит два временных слоя: верхний 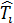и текущий T.

Задача состоит в переходе от известной функции Т к искомой 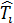на верхнем слое.

КРС (5) является явной потому что ее решение вычисляется по явным формулам

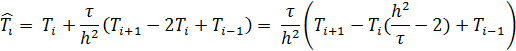
Распишем СЛАУ в неявную схему, заменив производную по времени назад.

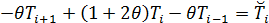, где ; ;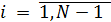

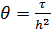T[0]=0; T[N] = .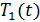

Ее можно переписать в матричном виде AT=F, где А матрица коэффициентов, Т искомая сеточная функция, F заданный вектор краевой задачи. .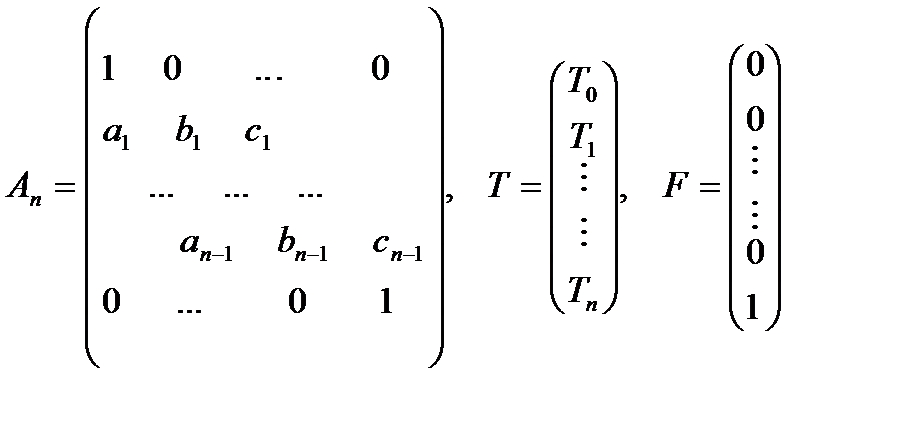

AT=F

Видим, что получили 3ехдиагональную матрицу, решаем ее методом прогонки(Томаса).

Он основывается на предположении, что искомые неизвестные связаны рекуррентным соотношением:

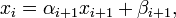где i=n-1…1

Где α,β – прогоночные коэффициенты:

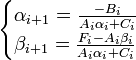
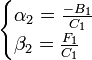
2) Результаты

Явная схема

N=51 – кол-во узлов

Зеленый график – T[N]

Синий график – T[0]

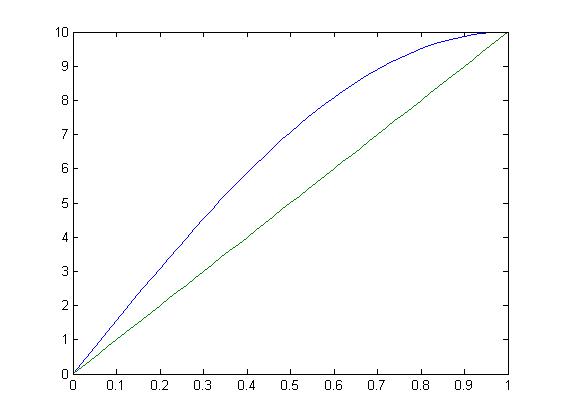
Неявная схема

N=51 – кол-во узлов

Зеленый график – T[N]

Синий график – T[0]

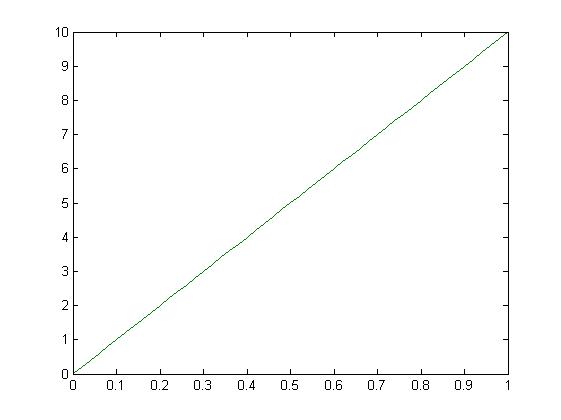
N=51 – кол-во узлов

Две схемы в узле T[N]

Зеленый график –явная схема.

Синий график – неявная схема.

Т.к. графики совпали – это сложновато увидеть

Перечень вопросов к практическим занятиям по биологии на осенний семестр