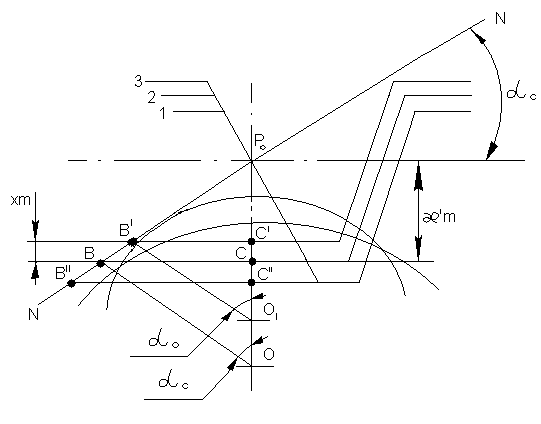
Рис.5.9. О подрезании зубьев колёс.
Рассмотрим, как связан коэффициент сдвига x рейки с числом зубьев, которое может быть нарезано рейкой на колесе. Пусть рейка установлена в положении 1(рис.5.9.). В этом случае прямая головок рейки пересечёт линию зацепления N-N в т. 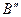 и нарезаемое колесо будет нарезано. Отодвинем рейку, сохраняя положение полюса
и нарезаемое колесо будет нарезано. Отодвинем рейку, сохраняя положение полюса 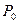 в положении 2 так, чтобы прямая головок проходила через крайнюю т. B теоретической линии зацепления. В этом случае колесо не будет подрезано и минимальное число зубьев Zmin, которое может быть нарезано, определится по формуле
в положении 2 так, чтобы прямая головок проходила через крайнюю т. B теоретической линии зацепления. В этом случае колесо не будет подрезано и минимальное число зубьев Zmin, которое может быть нарезано, определится по формуле 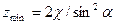 :
:
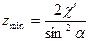 (5.21)
(5.21)
Отодвинем рейку ещё дальше от оси колеса в положение 3 на величину 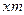 . Тогда прямая головок рейки пройдёт через т.
. Тогда прямая головок рейки пройдёт через т. 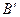 , и, следовательно, на колесе может быть без подрезания нарезано некоторое число зубьев z, меньшее, чем
, и, следовательно, на колесе может быть без подрезания нарезано некоторое число зубьев z, меньшее, чем 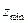 , подсчитанное по формуле (5.21).
, подсчитанное по формуле (5.21).
Выведем зависимость между 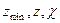 и
и 
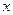 . Т.к. мы предложили, что полюс зацепления
. Т.к. мы предложили, что полюс зацепления 
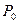 при сдвиге рейки не изменял своего положения, то из рис.9.9. следует, что основная окружность после сдвига будет иметь в качестве центра точку, которую мы получим, если в т.
при сдвиге рейки не изменял своего положения, то из рис.9.9. следует, что основная окружность после сдвига будет иметь в качестве центра точку, которую мы получим, если в т. 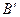 восстановим перпендикуляр к линии зацепления
восстановим перпендикуляр к линии зацепления 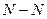 и найдём точку
и найдём точку 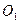 , как точку пересечения этого перпендикуляра с линией
, как точку пересечения этого перпендикуляра с линией 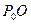 . Из подобия треугольников получим
. Из подобия треугольников получим
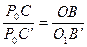
Так как 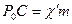 ,
, 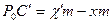 ,
, 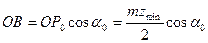 и
и 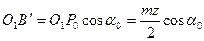 , то
, то 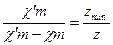 , или
, или 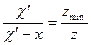 ;
;
Отсюда
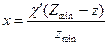 (5.22)
(5.22)
где 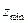 подсчитывается по формуле (9.21). Для угла зацепления
подсчитывается по формуле (9.21). Для угла зацепления 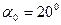 и коэффициент
и коэффициент 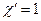 имеем
имеем
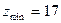 (5.23)
(5.23)
Для угла зацепления 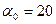 и
и 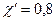
 (5.24)
(5.24)
и для угла зацепления 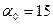 и
и 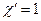
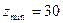 (5.25)
(5.25)
Для стандартного угла зацепления 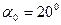 и
и 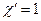 , воспользовавшись формулами (5.22) и (5.23), получаем выражение для коэффициента сдвига:
, воспользовавшись формулами (5.22) и (5.23), получаем выражение для коэффициента сдвига:
 (5.26)
(5.26)
Формула (5.26) позволяет создавать требуемую величину сдвига рейки для нарезания желательного числа зубьев без всякого их подрезания при угле зацепления 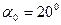 и
и 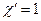 .
.
В современных расчётах допускают некоторый малый надрез, при котором срезается незначительная часть эвольвенты, и часто пользуются формулой
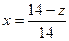 (9.27)
(9.27)
 2015-01-30
2015-01-30 1270
1270








