2015-01-30
561
Будем искать интерполяционный полином в виде:
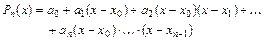. (5.15)
Значения коэффициентов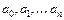 
найдем из условия совпадения значений исходной функции и многочлена в узлах. Полагая 
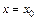, из (5.15) найдем 
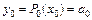, откуда 
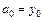. Далее последовательно придавая х значения 
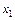и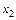 
, получаем:
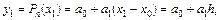
откуда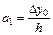 
;
,
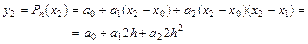т. е.
,
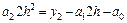или
,
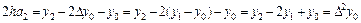откуда
.
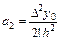Затем, проведя аналогичные выкладки, можно получить
.
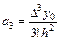В общем случае выражение для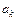 
будет иметь вид
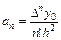. (5.16)
Подставляя (5.16) в выражение для многочлена (5.15), получаем
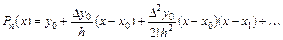
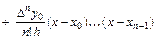(5.17)
Функция пакета MathCAD, возвращающая значения первого интерполяционного полинома Ньютона, представлена на рис. 5.4.
|
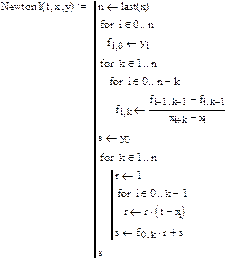
Рис. 5.4. Функция, возвращающая значения первого интерполяционного полинома Ньютона. Аргументы функции: t - координата точки; x - вектор, содержащий координаты узловых точек; y - вектор, содержащий значения интерполируемой функции в узловых точках
При ручных вычислениях формула (5.17) применяется несколько в ином виде. Положим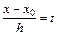 
, т.е. 
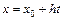, тогда:
,
,
…
.
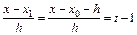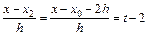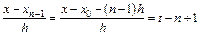Подставляя данные выражения в (5.17), окончательно получаем:
.
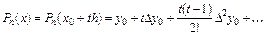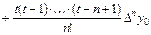. (5.18)
Формула (5.18) называется первой интерполяционной формулой Ньютона. Данная формула применяется для интегрирования в начале отрезка, когда t мало по абсолютной величине.
