План
5.1. Постановка задачи
5.2. Интерполяционный полином Лагранжа
5.3. Интерполяционный полином Ньютона для равноотстоящих узлов
5.3.1. Конечные разности
5.3.2. Первый интерполяционный полином Ньютона
5.3.3. Второй интерполяционный полином Ньютона
5.4. Погрешность метода многочленной интерполяции
5.5. Сплайн-интерполяция
5.1. Постановка задачи
Пусть известные значения некоторой функции f (x)образуют следующую таблицу:
Таблица 5.1
| x | x 0 | x 1 | … | xn |
| f (x) | y 0 | y 1 | … | yn |
Требуется получить значение функции f(x) для значения аргумента xÎ[x0,xn], несовпадающего ни с одним из значений хi (i = 0, 1,.., n).
Решение задачи находится отысканием некоторой приближающей функции F (x), близкой в некотором смысле к функции f (x), для которой известно аналитическое выражение.
Классический подход к решению задачи построения приближающей функции основан на требовании строгого совпадения значений функций f (x)и F (x) в точках 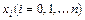
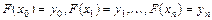 . (5.1)
. (5.1)
В данном случае нахождение приближенной функции называется интерполированием, а точки 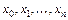 называются узлами интерполяции.
называются узлами интерполяции.
Будем искать интерполирующую функцию F (x) в виде многочлена степени n:
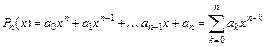 . (5.2)
. (5.2)
Условия (5.1), наложенные на многочлен, позволяют однозначно определить его коэффициенты. Действительно, требуя для 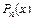 выполнения условий (5.1), получаем линейную систему, состоящую из
выполнения условий (5.1), получаем линейную систему, состоящую из 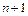 уравнения:
уравнения:
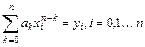 . (5.3)
. (5.3)
Решив систему (5.3) относительно неизвестных 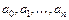 , находим значения этих неизвестных и, подставив в (5.2), находим аналитическое выражение аппроксимирующей функции.
, находим значения этих неизвестных и, подставив в (5.2), находим аналитическое выражение аппроксимирующей функции.
Система (5.4) всегда имеет единственное решение, т. к. ее определитель
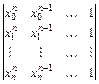 , (5.4)
, (5.4)
известный в алгебре как определитель Вандермонда, отличен от нуля.
Следовательно, интерполяционный многочлен 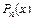 существует и единственен.
существует и единственен.
Документ пакета MathCAD, содержащий решение задачи интерполяции полиномом n -ой степени, состоит из следующих блоков.
1. Задание табличных значений интерполируемой функции
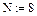
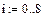
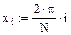
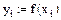
2. Визуализация табличной зависимости и истинных значений функции (рис. 5.1)
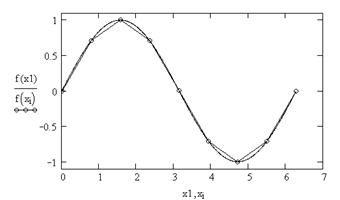
Рис. 5.1
3. Задание функции, возвращающей значения полинома (5.2)
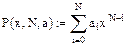
4. Задание функции, возвращающей значения элементов матрицы Вандермонда
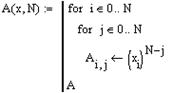
5. Вычисление значений элементов матрицы Вандермонда
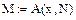
6. Вычисление коэффициентов полинома
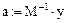
7. Построение разности между точным и интерполированными значениями функции (рис. 5.2)
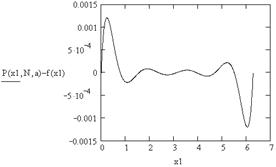
Рис. 5.2. Погрешность аппроксимации функции sin (x)
полиномом 8-й степени
Интерполяционный полином Лагранжа
Для функции, заданной табл. 5.1, построим интерполяционный многочлен 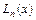 , степень которого не выше n и выполнены условия (5.1).
, степень которого не выше n и выполнены условия (5.1).
Будем искать 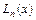 в виде
в виде
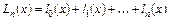 , (5.5)
, (5.5)
где 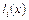 - многочлен степени n, причем
- многочлен степени n, причем
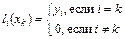 . (5.6)
. (5.6)
Очевидно, что требование (5.6) с учетом (5.5) обеспечивают выполнение условий (5.1).
Многочлены 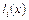 составим следующим способом:
составим следующим способом:
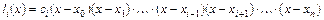 , (5.7)
, (5.7)
где 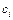 - постоянный коэффициент, значение которого находится из первой части условия (5.6):
- постоянный коэффициент, значение которого находится из первой части условия (5.6):
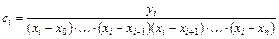 . (5.8)
. (5.8)
Подставив 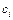 в (5.7) и далее в (5.5), окончательно получим:
в (5.7) и далее в (5.5), окончательно получим:
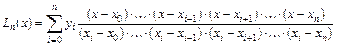 . (5.9)
. (5.9)
Формула (5.9) окончательно решает поставленную задачу.
Документ пакета MathCAD, содержащий решение задачи интерполяции полиномом Лагранжа состоит из следующих блоков.
1. Задание табличных значений интерполируемой функции
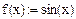
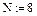
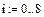
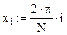
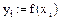
2. Задание функции, возвращающей значение многочлена 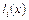 (рис. 5.3)
(рис. 5.3)
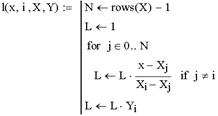
Рис. 5.3. Функция, возвращающая значение многочлена 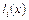 . Аргументы функции: x- координата точки; i - номер многочлена; X - вектор, содержащий координаты узловых точек; Y - вектор, содержащий значения интерполируемой функции в узловых точках
. Аргументы функции: x- координата точки; i - номер многочлена; X - вектор, содержащий координаты узловых точек; Y - вектор, содержащий значения интерполируемой функции в узловых точках
3. Задание функции, возвращающей значения полинома Лагранжа
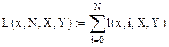
4. Построение разности между точными и интерполированными значениями функции (рис. 5.3)
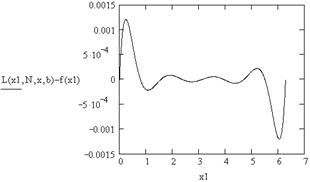
Рис. 5.3. Погрешность аппроксимации функции sin(x) полиномом
Лагранжа
 2015-01-30
2015-01-30 3008
3008