Когда значение аргумента находится ближе к концу отрезка интерполяции, используется вторая интерполяционная формула Ньютона, которая получается, если отыскивать интерполяционный полином в виде:
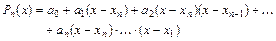 (5.19)
(5.19)
Коэффициенты полинома (5.19), находятся из условия совпадения значений функции и интерполяционного многочлена в узлах:
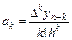 . (5.20)
. (5.20)
Функция пакета MathCAD, возвращающая значения второго интерполяционного полинома Ньютона, представлена на рис. 5.5.
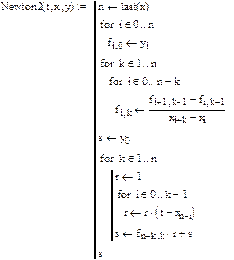 |
Рис. 5.5. Функция, возвращающая значения второго интерполяционного полинома Ньютона. Аргументы функции: t - координата точке; x - вектор, содержащий координаты узловых точек; y - вектор, содержащий значения интерполируемой функции в узловых точках
Подставив (5.20) в (5.19) и перейдя к переменной 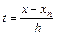 , получим окончательный вид интерполяционной формулы Ньютона, используемой при ручных вычислениях:
, получим окончательный вид интерполяционной формулы Ньютона, используемой при ручных вычислениях:
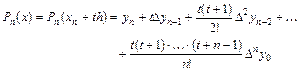 . (5.21)
. (5.21)
 2015-01-30
2015-01-30 1193
1193
