Определение расчетных расходов дождевых вод

Размеры сечений лотков, каналов и труб, служащих для отведения дождевых стоков, определяются по расчетному расходу, величина которого зависит от переменной величины интенсивности q (л/(с∙га)), величины коэффициента стока 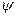и площади стока F (гa). Согласно методу предельных интенсивностей расход дождевых вод в рассматриваемом сечении будет максимальным, когда продолжительность расчетного дождя равна времени протока сточных вод от наиболее удаленной точки площади стока до рассчитываемого сечения T_p (мин).

Формула расчетной продолжительности дождя имеет следующий вид:

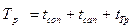(2.19)

Рассмотрим подробнее входящие в формулу (2.19) характеристики. Для этого проанализируем расчетную схему (рис. 2.4). На данном рисунке представлен квартал жилого массива, имеющий плоский рельеф местности. Согласно этой схеме, расчетная продолжительность дождя 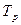равна времени добегания капли дождя от точки B до расчетного сечения А-А.

l_con

l_can

Рис. 2.4. Схема для определения расчетной продолжительности дождя 1 – дождевая уличная водоотводящая сеть; 2 – лоток; 3 – дождепремник; В –наиболее удаленная точка квартала;А-А– расчетное сечение

l_T_p

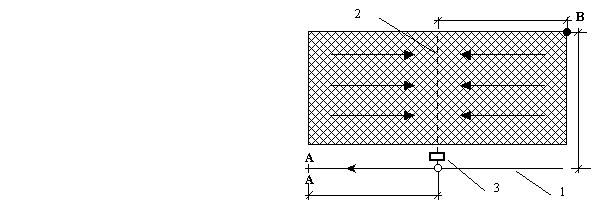
Таким образом, в формуле (2.19):

t_con – время протекания (время поверхностной концентрации)от наиболее удаленной точки до уличного лотка (на рис. 2.4 длина пути стока l_con), мин.Многочисленными подсчетами установлено, что в городских условиях среднее время протекания воды колеблется от 5 до 10 мин. СНиП 2.04.03-85 рекомендует это время принимать равным 3…5 мин при наличии внутриквартальных закрытых дождевых сетей, а при их отсутствии – 5…10 мин.

t_can – время протекания по уличному лотку до дождеприемника рассчитывается по выражению, мин:

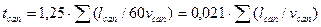, (2.20)

где 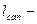длина участков лотков или канала (см. рис. 2.4), м; 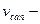скорость течения воды в конце участка, м/с. Поскольку скорость течения воды в лотках и каналах увеличивается при их наполнении, расчетное время протока по лотку должно быть несколько больше, чем время, определенное при максимальном расчетном расходе. Поэтому в формулу (2.20) введен коэффициент 1,25.

t_T_p – время протекания по трубам от дождеприемника до расчетного сечения (время протока воды по дождевой сети) принимается как сумма времени протока по отдельным участкам при расчетных для каждого участка расходах, мин:

t_T_p = 0,017Σ(l_T_p / v_T_p), (2.21)

где l_T_p – длина расчетных участков коллектора (см. рис. 2.4), м; v_T_p – расчетные средние скорости на участках, м/с.

Таким образом, продолжительность дождя, по которой принимают соответствующую его интенсивность, можно представить в виде:

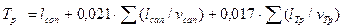(2.22)

Учитывая то, что q_T = A / Т_p, расход дождевых вод по формуле предельной интенсивности стока будем определяться:

Q_max = Ψ∙F∙A/T_p, (2.23)

или

при постоянном значении коэффициента стока:

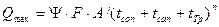, (2.24)

при переменном значении коэффициента стока:

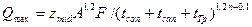, (2.25)

При расчете по методу предельных интенсивностей в момент максимального расхода в расчетном сечении коллектора на верхних участках возникает свободная емкость. Поэтому расчет дождевых коллекторов ведут не на максимальный, а на расчетный расход:

Q_cоl = β_eηQ_max, (2.26)

где β_e – коэффициент, учитывающий заполнение свободной емкости коллектора, зависит от n и уклона местности i может быть принят по приложению 5 или рассчитываться по ниже представленным схемам в зависимости от типа дождя; η – коэффициент неравномерности выпадения дождя принимается по приложение 6.

Итак, особенностью формирования дождевых стоков в канализационных коллекторах является не одновременность возникновения расчетных (максимальных) расходов на разных их участках. Нижние участки труб рассчитаны на большее время протекания, а значит, на дождь большей продолжительности, следовательно, меньшей интенсивности. Тогда при выпадении этого дождя верхние участки будут заполняться не полностью, т.к. они рассчитаны на меньшую продолжительность, следовательно, на большую интенсивность дождя.

Поэтому при возникновении расчетного расхода на одном участке, другие будут работать с неполным заполнением.

Учет свободной емкости (см. формулу 2.26) при расчете производится с помощью коэффициента β_e:

β_e = Q_p / Q_max, (2.27)

где Q_p - расчетный расход, Q_max - максимальный расход, л/с.

Значения коэффициента β_e зависят от того, каким образом происходит изменение интенсивности дождя во время его выпадения. Возможны 5 типов дождей:

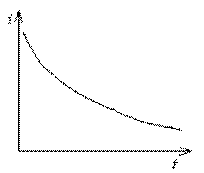1. Интенсивность дождя максимальна в начале (рис. 2.5): Вероятность выпадения такого дождя – 37%. Гидрограф стока описывается зависимостью:

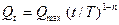(2.28)

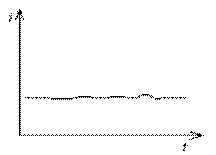Рис. 2.5. Гидрограф дождя с максимальной интенсивностью в начале

где Q_max = AF / Tⁿ, T - полное время добегания, мин. Коэффициент свободной емкости: β_I = 1- n.

2. Интенсивность дождя равномерна (рис. 2.6): Вероятность выпадения такого дождя – 11%. Гидрограф стока описывается зависимостью:

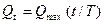(2.29)

Коэффициент свободной емкости: β_II = 1-0,5 n.

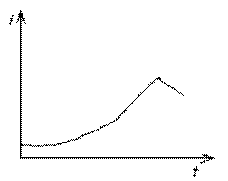Рис. 2.6. Гидрограф дождя с равномерной интенсивностью

3. Интенсивность максимальна в конце дождя (рис. 2.7): Вероятность выпадения такого дождя – 13%. Гидрограф стока описывается зависимостью:

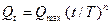(2.30)

Рис. 2.7. Гидрограф дождя с максимальной интенсивностью в конце

Коэффициент свободной емкости: β_III = 4/3(1-0,5 n).

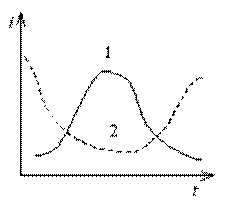4. Интенсивность максимальна в середине (1) или два максимума (2) (рис. 2.8):

Вероятность выпадения соответственно – 28% и 11%.

Коэффициент свободной емкости:

β_IV = β_V = 1-0,5 n.

Рис. 2.8. Гидрограф дождя с максимальной интенсивностью в середине (1) и двумя максимумами (2)

Если рассчитать общий коэффициент β как

средневзвешенное значение коэффициентов по

вероятностям, то: β_e = 1-0,7 n, если каждый дождь

считать равновероятным, то: β_e = 1-0,5 n.

Таким образом, используя коэффициент β_e, можно уменьшить расчетный расход (см. формулу 2.25) или, наоборот, уменьшить уклон трубопровода при старом диаметре:

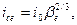(2.31)