Обратимся к уравнению температурного поля в бесконечной тонкой пластине. Первый сомножитель в этой формуле обозначим через 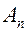 , а второй –
, а второй – 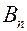 :
:
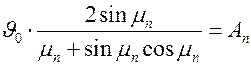 ,
, 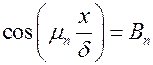 ,
,
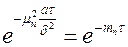 , где
, где 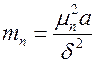 .
.
Тогда формула запишется в виде 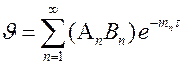 .
.
Для тел других, нежели пластина, форм температурное поле будет описываться уравнением такого же вида, другие будут только 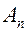 и
и 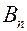 .
.
При охлаждении тел могут иметь место три стадии (режима), отличающиеся скоростью изменения температуры тела. Неупорядоченная стадия процесса охлаждения – это первая стадия, при которой скорость изменения температуры внутри тела зависит от начального вида распределения температуры. Третья стадия – стационарная стадия, когда температура во всех точках тела остается постоянной во времени и равна температуре окружающей среды. Вторая стадия, или регулярный тепловой режим, наступает тогда, когда начальные условия процесса охлаждения играют второстепенную роль. Процесс полностью определяется только условиями охлаждения на границе тела и среды, физическими свойствами тела, его геометрической формой и размерами. Температурное поле в этом случае описывается первым членом ряда
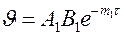 .
.
Логарифмируя выражение и опуская индексы, получим
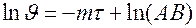 .
.
Из формулы следует, что натуральный логарифм избыточной температуры для всех точек тела изменяется во времени по линейному закону.
Продифференцируем выражение по времени: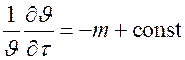 . Величину
. Величину 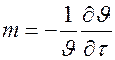 называют темпом охлаждения.
называют темпом охлаждения.
Темп охлаждения m, 1/c, характеризует относительную скорость изменения температуры в теле и зависит только от физических свойств тела, процесса охлаждения на его поверхности, геометрической формы и размеров тела.
Теория регулярного режима дает простой и достаточно точный метод определения теплофизических коэффициентов вещества 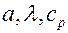 и коэффициента теплоотдачи
и коэффициента теплоотдачи 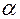 . В основе метода лежат две так называемые теоремы Кондратьева.
. В основе метода лежат две так называемые теоремы Кондратьева.
Первая теорема Кондратьева. Теорема позволяет найти зависимость темпа охлаждения m от физических свойств тела, его геометрической формы и размеров, а также условий теплообмена на поверхности тела.
Запишем тепловой баланс между количеством теплоты 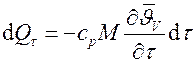 , отданным телом при охлаждении, и теплотой
, отданным телом при охлаждении, и теплотой 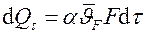 , полученной средой, в которой тело охлаждается.
, полученной средой, в которой тело охлаждается.
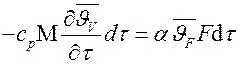 ,
,
где знак (–) свидетельствует, что теплота отводится с поверхности тела; 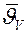 и
и 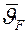 – средняя по объему и поверхности тела избыточная температура соответственно. Умножим левые и правые части выражения на
– средняя по объему и поверхности тела избыточная температура соответственно. Умножим левые и правые части выражения на 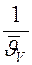 , сократим на d t и, учтя, что M = r·V, получим аналитическую запись первой теоремы Кондратьева:
, сократим на d t и, учтя, что M = r·V, получим аналитическую запись первой теоремы Кондратьева:
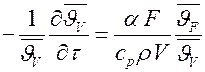 или
или 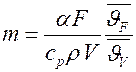 .
.
Темп охлаждения однородного и изотропного тела пропорционален коэффициенту теплоотдачи, площади поверхности тела и обратно пропорционален удельной теплоемкости, плотности и объему тела.
Отношение 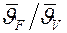 называется коэффициентом неравномерности распределения температуры в теле и зависит от условий охлаждения на поверхности тела. При Bi ® 0 (Bi < 0,1)
называется коэффициентом неравномерности распределения температуры в теле и зависит от условий охлаждения на поверхности тела. При Bi ® 0 (Bi < 0,1) 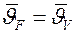 , а
, а 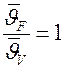 . При Bi ® ¥ (Bi > 100)
. При Bi ® ¥ (Bi > 100) 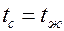 , а
, а 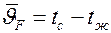 , значит,
, значит, 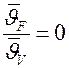 .
.
Вторая теорема Кондратьева. При Bi ® ¥ (или то же, что a®¥) темп охлаждения становится пропорционален коэффициенту температуропроводности а.
Темп охлаждения 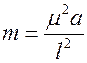 . При
. При 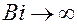 для пластины
для пластины 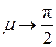 . Тогда
. Тогда 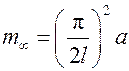 . Обозначим
. Обозначим 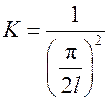 . Напомним, что для пластины характерным линейным размером является половина толщины пластины (
. Напомним, что для пластины характерным линейным размером является половина толщины пластины (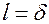 ). Поэтому для пластины K – коэффициент формы запишется в виде
). Поэтому для пластины K – коэффициент формы запишется в виде 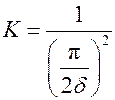 . Для тел другой геометрической формы:
. Для тел другой геометрической формы:
• для цилиндра радиусом 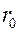 и высотой
и высотой 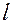
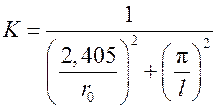 ;
;
• для параллелепипеда 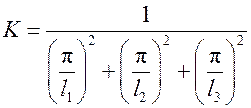 ;
;
• для шара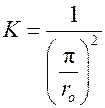 .
.
Подставим коэффициент формы в формулу темпа охлаждения
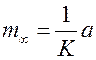 , откуда получим, что
, откуда получим, что
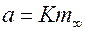 .
.
Лекция 7. Раздел 5. Конвективный теплообмен
 2014-04-09
2014-04-09 8390
8390








