2014-04-09
4263
Любое тело конечных размеров правильной геометрической формы можно получить путем пересечения бесконечных тел. Например, цилиндр конечных размеров, можно получить путем пересечения бесконечного цилиндра диаметром 2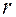
и бесконечной пластины толщиной 2d.
Для нахождения распределения температуры в теле конечных размеров необходимо воспользоваться теоремой о перемножении решений. Теорема гласит: безразмерная температура тела конечных размеров в данной точке в данный момент времени равна произведению безразмерных температур в той же точке и в тот же момент времени бесконечных тел, в результате пересечения которых образовалось данное тело конечных размеров. Доказательство этой теоремы можно найти в [1].
Например, пусть необходимо найти температуру в точке 1, лежащей на поверхности бесконечного цилиндра и в центре бесконечной пластины (см. рис.1.21), в результате пересечения которых получен цилиндр конечных размеров. Решение запишется в виде
,
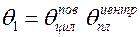где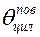 
– безразмерная температура на поверхности бесконечного цилиндра, определяется как функция Bi и Fо для цилиндра 
; 
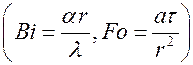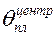– безразмерная температура в центре бесконечной пластины, являющаяся функцией также Bi и Fо, но для пластины 
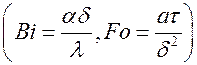. Находя по соответствующим графикам 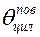и 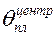, определяют безразмерную температуру 
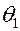, а затем искомую температуру 
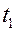в точке 1.
.
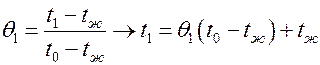Охлаждение (нагревание) тел любой формы с Bi ® 0 (Bi £ 0,1)
Если при решении задач нестационарной теплопроводности число Bi получается очень маленьким, то пользоваться вышеупомянутыми графиками для определения температуры тела почти невозможно (очень мала точность). В этом случае можно воспользоваться несложным аналитическим решением, которое получим ниже.
Постановка задачи. Пусть имеем тело, поверхность которого F, а объем V. В момент времени t = 0 избыточная температура тела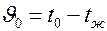 
. Тело охлаждается в среде с 
= const и a = const. Требуется найти закон распределения температуры в зависимости от объема и формы тела.
При Bi ® 0 температура всех точек тела в данный момент времени одинакова. Теплота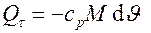 
, отдаваемая телом (поэтому знак минус), отводится в окружающую среду –
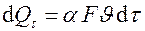. Значит,
.
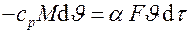Разделяя переменные и интегрируя, получаем
, 
.
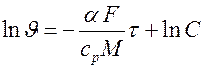Найдем постоянную интегрирования. Запишем начальные условия: при t = 0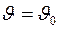 
. Подставляя начальные условия, получаем 
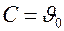. Тогда
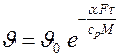или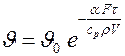 
,
так как M = r·V. Уравнение представляет собой закон изменения температуры в теле. Запишем этот закон для тел правильной формы:
• Для пластины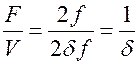 
. Подставим это в показатель степени 
,
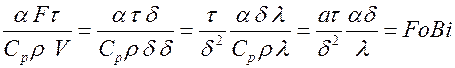где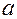 
– коэффициент температуропроводности, 
,
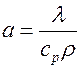тогда
;
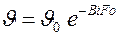• для цилиндра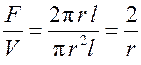 
. Делая преобразования, аналогичные показанным выше, получим
;
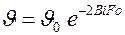• для шара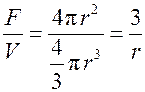 
получим
.
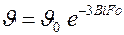Из приведенных уравнений следует, что при одинаковой величине определяющего геометрического размера и прочих равных условиях наибольшая скорость изменения температуры – у шара.
