Дифференциальное уравнение теплопроводности

Процесс распространения теплоты теплопроводностью математически описывается дифференциальным уравнением, выведенным на основе закона сохранения энергии.

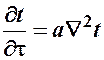; (6) –

Дифференциальное уравнение теплопроводности в неподвижной среде. 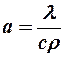- коэффициент температуропроводности; характеризует теплоинерционные свойства вещества. Чем больше 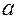, тем тело быстрее охлаждается (нагревается).

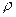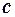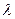, , - не изменяются по направлению и во времени.

Для стационарных процессов - 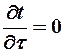,т.е. температура не меняется со временем и уравнение (6) принимает вид 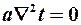. Т.к. а¹0, то 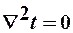(7)

или 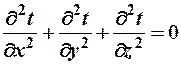- Дифференциальное уравнение теплопроводности в неподвижной среде при стационарном тепловом режиме. Уравнения (6) и (7) дают возможность решать задачи связанные с распространением тепла в теле путем теплопроводности как при стационарном, так и при нестационарном тепловом режиме. При решении конкретных задач уравнения дополняются соответствующими начальными и граничными условиями.