Программирования. Прямая и двойственная задачи

Для каждой задачи линейного программирования можно составить двойственную задачу линейного программирования.

Допустим, прямая задача состоит в нахождении максимального значения функции:

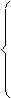f(x) = 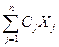® max, (1.17)

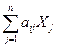£ b_i; (i = 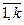), (1.18)

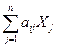= b_i; (i = 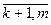), (1.19)

Х _j ³ 0; (j = 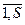; S £ n). (1.20)

Тогда двойственная задача по отношению к задаче (1.17) – (1.20) состоит в нахождении минимального значения функции:

F(Y) = 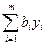® min, (1.21)

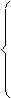
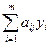³ C _j; (j = 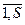), (1.22)

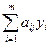= C _j; (j = 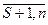), (1.23)

y _i ³ 0; (i = 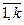; k £ m). (1.24)

Правила составления двойственной задачи:

1. Если функция исходной задачи 1.17 – 1.20 задается на максимум, то целевая функция двойственной к ней задачи (1.21) – (1.24) задается на минимум.

2. Матрица

А = ,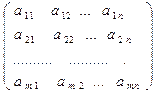

составленная из коэффициентов при неизвестных в системе ограничений (1.18) и (1.19), и матрица, составленная из коэффициентов при неизвестных в системе ограничений (1.22) и (1.23), являются транспонированными по отношению друг к другу (то есть столбцы в этих матрицах меняются местами со строками):

А = .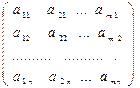

3. Число переменных в двойственной задаче равно числу ограничений в исходной, и наоборот, число ограничений двойственной задачи равно числу переменных исходной.

4. Коэффициенты при переменных в целевой функции прямой задачи становятся свободными членами (правыми частями) системы ограничений двойственной задачи. А правые части в соотношениях системы ограничений прямой задачи становятся коэффициентами при переменных в целевой функции двойственной задачи.