Рассмотрим следующую задачу: найти такие значения переменных Х1 и Х2, которые максимизируют функцию цели
f(x) = C1 × Х1 + C2 × Х2 ® max (1.14)
при выполнении ограничений
аi1 × Х1 + аi2 × Х2 £ bi; (i = 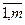 ); (1.15)
); (1.15)
условие неотрицательности Х1 ³ 0, Х2 ³ 0. (1.16)
Каждое неравенство (1.15) и (1.16) системы ограничений геометрически представляет собой полуплоскость с граничными прямыми:
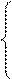 аi1 × Х1 + аi2 × Х2 = bi (i =
аi1 × Х1 + аi2 × Х2 = bi (i = 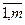 ),
),
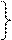
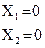
- оси координат (решение
получаем в 1 квадранте).
В том случае, если система неравенств (1.15) и (1.16) совместна, то область ее решений есть множество точек, принадлежащих всем указанным полуплоскостям. А так как множество точек пересечения данных полуплоскостей – выпуклое, то область допустимых решений задачи (1.14) – (1.16) есть выпуклое множество, которое называется многоугольником решений. Стороны этого многоугольника лежат на прямых, уравнения которых получают из исходной системы ограничений заменой знаков неравенств на знаки точных равенств. Таким образом, исходная задача линейного программирования состоит в нахождении такой точки многоугольника решений, в которой функция цели f(x) принимает максимальное значение. Эта точка существует тогда, когда многоугольник решений не пуст и функция цели ограничена сверху.
При указанных условиях в одной из вершин многоугольника функция цели принимает максимальное значение. Для определения данной вершины строится вектор-нормаль с координатами – коэффициентами функции цели 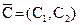 . Перпендикулярно вектору-нормали построим линию уровня C1 × Х1 + C2 × Х2 = h (где h – некоторое число, которое подбирается таким, чтобы эта линия уровня проходила через многоугольник решений). Будем передвигать линию уровня в направлении вектора–нормали до тех пор, пока она не дойдет до последней общей точки с многоугольником решений. Координаты этой точки и определяют оптимальный план – решение задачи.
. Перпендикулярно вектору-нормали построим линию уровня C1 × Х1 + C2 × Х2 = h (где h – некоторое число, которое подбирается таким, чтобы эта линия уровня проходила через многоугольник решений). Будем передвигать линию уровня в направлении вектора–нормали до тех пор, пока она не дойдет до последней общей точки с многоугольником решений. Координаты этой точки и определяют оптимальный план – решение задачи.
Координаты этой точки А 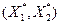 находятся следующим образом: решается система уравнений, которые соответствуют линиям-ограничениям, на пересечении которых эта точка находится. Подставляя значения координат этой точки в функцию цели, получаем максимальное значение целевой функции. Для нахождения минимума функции цели линия уровня передвигается не в направлении вектора-нормали, а в противоположном направлении.
находятся следующим образом: решается система уравнений, которые соответствуют линиям-ограничениям, на пересечении которых эта точка находится. Подставляя значения координат этой точки в функцию цели, получаем максимальное значение целевой функции. Для нахождения минимума функции цели линия уровня передвигается не в направлении вектора-нормали, а в противоположном направлении.
При нахождении решения задачи (1.14) – (1.16) возможны следующие случаи:
1. Единственное оптимальное решение – в точке А функция цели принимает максимальное значение
 Х2
Х2
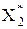 А
А
- линия уровня
С2 (f(х) ® max)
f(х) = 0 - область
вектор- допустимых значений
нормаль 0 С1  Х1
Х1
2. Множество точек на отрезке DВ – оптимальное решение
 Х2 линия уровня (f(х) ® min)
Х2 линия уровня (f(х) ® min)
|
A
D
В
0 Х1
3. Функция цели не ограничена сверху на множестве допустимых решений
 Х2
Х2
- линия уровня (f(х)max = + ¥)
0 Х1
4. Система ограничений задачи несовместна. Условия противоречивы. Многоугольник решений пуст. Решения нет.
 Х2
Х2
Х1
Пример. Найти решение задачи графическим и аналитическим методами:
f(x) = 2X1 + X2 ® max,
 –2X1 + X2 £ 2,
–2X1 + X2 £ 2,
X1 + X2 £ 4,
X1 – X2 £ 1,
X1 ³ 0, X2 ³ 0.
Решение.
 |
Построим прямые, уравнения которых получаем в результате замены в системе ограничений знаков неравенств на знаки точных равенств. Получаем уравнения прямых линий на плоскости. Для того, чтобы провести прямую линию, достаточно знать координаты двух точек. Проведем линию (1), соответствующую первому ограничению. Для этого присвоим переменной Х2 некоторое значение, например ноль, и определим значение переменной Х1, найдем координаты первой точки (-1; 0). Приравняв нулю переменную Х1, найдем значение переменной Х2 – координаты второй точки (0; 2). Для того, чтобы определить, с какой стороны от проведенной линии находится область допустимых значений, необходимо подставить в неравенство координаты какой-нибудь точки пространства, например начала координат (Х1 = 0, Х2 = 0). Полученное значение – ноль, меньше чем два (правая часть ограничения), а значит, точка начала координат принадлежит искомой полуплоскости. Повторим построения для всех остальных ограничений задачи и получим многоугольник решений ОDАВЕ. Построим вектор-нормаль, выходящий из начала координат в направлении точки с координатами – коэффициентами функции цели (Х1 = 2, Х2 = 1) или пропорциональными этим координатам (Х1 = 1, Х2 = 0,5). Линия уровня (соответствующая функции цели) строится перпендикулярно вектору-нормали или же функция цели приравнивается какому-либо числу, например f(x) = 2X1 + X2 = 2 и проводится соответствующая линия. Передвинем линию уровня в направлении, указанном вектором. В результате находим точку А, в которой целевая функция принимает максимальное значение. Находим координаты этой точки. Для этого решим систему уравнений, которые соответствуют прямым, на пересечении которых находится точка А:
 X1 + X2 = 4,
X1 + X2 = 4,
X1 - X2 = 1.
Проведем сложение двух уравнений, получим
2X1 = 5, откуда X1 = 2,5.
Вычтем из первого уравнения второе, получим
2X2 = 3, откуда X2 = 1,5.
Вычислим значение функции цели в точке А(2,5; 1,5)
f(x)max = 2 × 2,5 + 1,5 = 6,5.
 2015-01-30
2015-01-30 418
418








