Если не соблюдается баланс предложения и спроса, то есть
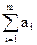 ¹
¹ 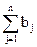 ,
,
то такая задача называется открытой. Для решения такой задачи, если общее предложение превышает общий спрос, то есть
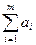 >
> 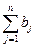 ,
,
необходимо ввести в модель фиктивный пункт потребления (Вn+1) в n + 1-м столбце матрицы транспортной задачи. При этом стоимости перевозки для фиктивного пункта потребления равны нулю:
Ci,n+1 = 0; i = 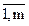 .
.
Потребность в грузе фиктивного пункта назначения равна разности предложения и спроса.
Таблица 2.8
| Пункты отправления | Пункты назначения | Запасы (предложение) | |||||
| В1 | … | Вj | … | Вn | (Вn+1) | ||
| А1 | С11 | C1j | C1n | а1 | |||
| … | … | … | |||||
| Аi | Сi1 | Сij | Сin | аi | |||
| … | … | … | |||||
| Аm | Сm1 | Сmj | Сmn | аm | |||
| Потребности (спрос) | b1 | … | bj | … | bn | (bn+1 = Sаi - Sbj) |
Если величина суммарного спроса превышает суммарное предложение, то есть
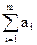 <
< 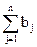 ,
,
необходимо ввести в модель фиктивный пункт отправления грузов (Аm+1) в m + 1-ю строку матрицы транспортной задачи. При этом стоимости перевозки от фиктивного пункта отправления равны нулю:
Cm+1,j = 0; j = 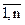 .
.
Предложение фиктивного пункта отправления равно разности суммы потребностей и запасов грузов.
Таблица 2.9
| Пункты отправления | Пункты назначения | Запасы (предложение) | ||||
| В1 | … | Вj | … | Вn | ||
| А1 | С11 | C1j | C1n | а1 | ||
| … | … | … | ||||
| Аi | Сi1 | Сij | Сin | аi | ||
| … | … | … | ||||
| Аm | Сm1 | Сmj | Сmn | аm | ||
| (Аm+1) | (am+1 = Sbj - Sаi) | |||||
| Потребности (спрос) | b1 | … | bj | … | bn | __ |
Определение оптимального плана транспортных
 2015-01-30
2015-01-30 544
544








