Транспортной задачи

Пусть дан некоторый опорный план. Для каждой свободной клетки таблицы перевозок вычислим алгебраические суммы стоимостей в вершинах цикла D_ij. Так, для клетки (4,1) получим

D₄₁ = 6 – 5 + 4 – 3 + 1 – 2 = 1.

Если все D_ij неотрицательны (D_ij ³ 0), то задача решена, т.е. найден оптимальный план перевозок.

Допустим, есть хотя бы одно отрицательное значение D_ij, тогда среди отрицательных D_ij выбираем наименьшее и для этой клетки i₀, j₀ делаем сдвиг по циклу пересчета на величину q₀, равную наименьшей из перевозок, стоящих в отрицательных вершинах цикла. Полученный новый опорный план будет лучше предыдущего, при этом целевая функция уменьшится на величину q₀ × .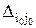

Замечания:

1. Каждая сумма D_ij начинается с положительного числа и кончается отрицательным. Количество всех слагаемых четное.

2. Если опорный план вырожденный, то возможен сдвиг по циклу пересчета на величину q = 0. При этом значение целевой функции не изменится, а изменятся базисные клетки.

Найдем решение задачи, первоначальный опорный план которой получен методом северо-западного угла, и введем дополнительное условие: груз из пункта А₂ в пункт В₃ не может быть доставлен:

	В1	В2	В3	В4		Для всех свободных клеток вычислим Dij: D13 = 2 – 1 + 3 – 4 = 0, D14 = 5 – 1 + 2 – 1 + 3 – 4 = = 4, D21 = 6 – 5 + 4 – 1 = 4, D23 = М – 1 + 3 – 1 = = М + 1, D24 = 3 – 1 + 2 – 1 + 3 – 1 = = 5,
А1	- 5 20	+ 4 10	2	5
А2	6	1 70	М	3
А3	+ 2 q	- 3	1 40	8
А4	6	3	2 30	1 70

D₃₁ = 2 – 3 + 4 – 5 = -2, D₃₄ = 8 – 1 + 2 – 1 = 8,

D₄₁ = 6 – 5 + 4 – 3 + 1 – 2 = 1, D₄₂ = 3 – 3 + 1 – 2 = -1.

Поскольку не все D_ij ³ 0, план перевозок не оптимален. Среди D_ij < 0 выбираем наименьшее. Это D₃₁ = -2. Делаем сдвиг по циклу пересчета для свободной клетки (3,1) на величину q₀. Этот цикл проходит через базисные клетки (1,1), (1,2) и (3,2). В этом цикле две отрицательные клетки (1,1) и (3,2). Им соответствуют перевозки 20 и 10. В качестве q₀ выбираем меньшее из этих чисел, т.е. q₀ = 10. После сдвига по циклу пересчета на величину q₀ переходим к следующему опорному плану:

	В1	В2	В3	В4		Делаем второй шаг распределительного метода. Находим значения Dij для всех свободных клеток D13 = 2 – 5 + 2 – 1 = -2, D14 = 5 – 1 + 2 – 1 + 2 – 5 = = 2, D21 = 6 – 5 + 4 – 1 = 4, D23 = М – 1 + 4 – 5 + 2 - 1 = М – 1 >> 0,
А1	- 5 10	4 20	+ 2 q	5
А2	6	1 70	М	3
А3	+ 2 10	3	- 1 40	8
А4	6	3	2 30	1 70

D₂₄ = 3 – 1 + 4 – 5 + 2 – 1 + 2 – 1 = 3,

D₃₂ = 3 – 4 + 5 – 2 = 2,

D₃₄ = 8 – 1 + 2 – 1 = 8,

D₄₁ = 6 – 2 + 1 – 2 = 3,

D₄₂ = 3 – 4 + 5 – 2 + 1 – 2 = 1.

f(х) = 10 × 5 + 20 × 4 + 70 × 1 + 10 × 2 + 40 × 1 + 30 × 2 + 70 × 1 = 390.

Делаем сдвиг по циклу пересчета для свободной клетки (1,3) на величину q₀ = 10. Переходим к новому опорному плану:

	В1	В2	В3	В4		Найдем Dij для этой таблицы D11 = 5 – 2 + 1 – 2 = 2, D14 = 5 – 2 + 2 – 1 = 4, D21 = 6 – 1 + 4 – 2 + 1 – 2 = 6, D23 = М – 2 + 4 – 1 = = М + 1, D24 = 3 – 1 + 4 – 2 + 2 – 1 = 5, D32 = 3 – 4 + 2 – 1 = 0, D34 = 8 – 1 + 2 – 1 = 8,
А1	5	- 4 20	+ 2 10	5
А2	6	1 70	М	3
А3	2 20	3	1 30	8
А4	6	+ 3 q	- 2 30	1 70

D₄₁ = 6 – 2 + 1 – 2 = 3, D₄₂ = 3 – 4 + 2 – 2 = -1.

f(х) = 20 × 4 + 10 × 2 + 70 × 1 + 20 × 2 + 30 × 1 + 30 × 2 + 70 × 1 = 370.

Делаем сдвиг по циклу пересчета для свободной клетки (4,2) на величину q₀ = 20.

Переходим к новому опорному плану:

	В1	В2	В3	В4		Определим значения Dij D11 = 5 – 2 + 1 – 2 = 2, D12 = 4 – 2 + 2 – 3 = 1, D14 = 5 – 1 + 2 – 2 = 4, D21 = 6 – 1 + 3 – 2 + 1 – 2 = = 5, D23 = М – 1 + 3 – 2 = = М >> 0, D24 = 3 – 1 + 3 – 1 = 4, D32 = 3 – 3 + 2 – 1 = 1,
А1	5	4	2 30	5
А2	6	1 70	М	3
А3	2 20	3	1 30	8
А4	6	3 20	2 10	1 70

D₃₄ = 8 – 1 + 2 – 1 = 8, D₄₁ = 6 – 2 + 1 – 2 = 3.

f(х) = 30 × 2 + 70 × 1 + 20 × 2 + 30 × 1 + 20 × 3 + 10 × 2 + 70 × 1 = 350.

Для этого плана все D_ij > 0. Следовательно, этот опорный план оптимальный.

Для расчёта задач транспортного типа в среде Excel (рис. 17) необходимо ввести в таблицу тарифы на перевозку единицы груза по различным маршрутам (например, в ячейки B3:Е6), величину предложения поставщиков (например, в ячейки F3:F6) и величину спроса потребителей (например, в ячейки B7:Е7). Для размещения искомых значений переменных необходимо зарезервировать свободные ячейки (например, ячейки B9:Е12). Математические выражения для системы ограничений по спросу и предложению вводятся (например, в ячейки F9:F12 и B13:E13 соответственно) с помощью функции СУММ (рис. 18). Целевая функция вводятся (например, в ячейку F13) с помощью функции СУММПРОИЗВ из категории Математические (рис. 19). Для этого необходимо выбрать в меню Вставка строку Функция….

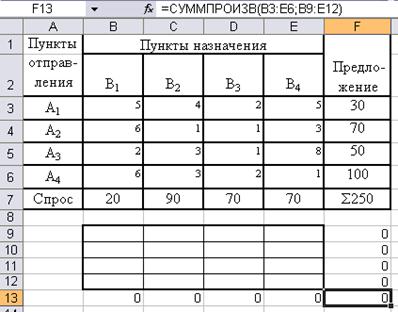
Рис. 17. Ввод исходных данных транспортной задачи в Excel

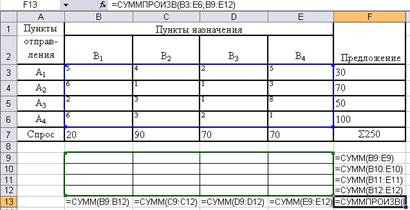
Рис. 18. Табличное представление транспортной задачи в Excel

Аргументами функции СУММПРОИЗВ являются: Массив1 - адреса матрицы тарифов перевозок, Массив2 – адреса пустых ячеек, зарезервированных под размещение искомых переменных задачи (плана перевозок).

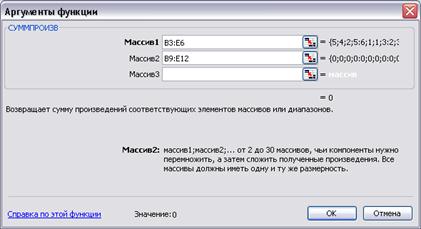
Рис. 19. Ввод целевой функции транспортной задачи

Условия транспортной задачи вводятся в диалоговую форму надстройки Поиск решения, вызываемой из меню Сервис (рис. 20). В окно Установить целевую ячейку вводится адрес функции цели щелчком левой кнопки мышки по ячейке, содержащей математическое выражение для подсчёта общих затрат на перевозки. Направление поиска экстремума целевой функции устанавливается соответствующим минимальному значению. В окно Изменяя ячейки вводятся адреса искомых значений переменных (B9:Е12).

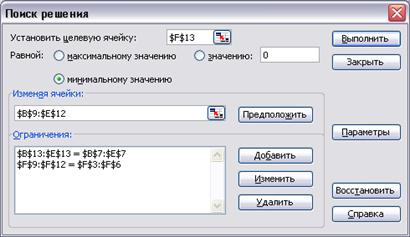
Рис. 20. Заполнение диалоговой формы Поиск решения

Ограничения задачи добавляются, изменяются и удаляются после нажатия соответствующей кнопки. В двух последних случаях предварительно необходимо выделить требуемую строку в окне Ограничения.

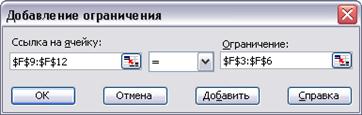
Рис. 21. Заполнение диалоговой формы Добавление ограничения

В левом окне формы Добавление ограничения (рис. 21) вводятся адреса левой части ограничений – суммы объёмов перевозок от поставщиков и суммы объёмов перевозок к потребителям. Знак ограничения устанавливается в виде знака равенства “ =“. В правом окне формы Добавление ограничения вводятся адреса правой части ограничений – числовые значения предложения и спроса.

Нажав кнопку Параметры, следует поставить «галки», выделив пункты: Линейная модель, Неотрицательные значения и Автоматическое масштабирование (рис. 22).

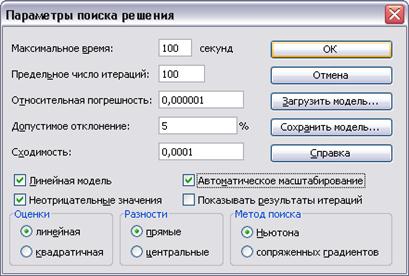
Рис. 22. Заполнение диалоговой формы Параметры

Оптимальный план перевозок представлен на рис. 23. Так, от первого поставщика третьему потребителю перевозится 30 единиц груза, от второго поставщика второму потребителю – 70 единиц груза. Третий поставщик обеспечивает поставки первому потребителю в объёме 20 единиц груза и третьему потребителю – 30 единиц груза. Поставки из четвёртого пункта отправления осуществляются по трём маршрутам: второму потребителю – 20 единиц груза, третьему потребителю – 10 единиц груза, третьему – 70 единиц груза. Общие затраты на перевозки составят 350 ден.ед.

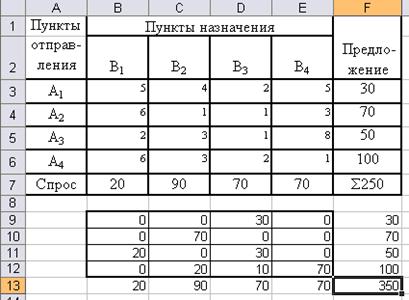
Рис. 23. Результаты решения транспортной задачи